已知抛物线y2=8x,过M(2,3)作直线l交抛物线于A、B.
(1)求以M(2,3)为中点的弦AB所在直线l的方程.
(2)设AB的中点为N,求N的轨迹方程.
解:(1)由题知l的斜率存在设斜率为且k≠0,设A(x
1,y
1),B(x
2,y
2),∵A、B在y
2=8x上,
∴
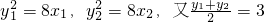
,
∴由 (y
1+y
2)(y
1-y
2)=8(x
1-x
2),可得
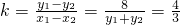
,
故AB所在直线l的方程为:y-3=

(x-2),即 4x-3y+1=0.
(2)设AB的中点N(x
0,y
0 ),A(x
1,y
1) B (x
2,y
2),∴
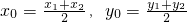
.
当l斜率存在时,设斜率为k,直线方程为:y-3=k(x-2),∵A、B在y
2=8x上,
∴y
12=8x
1,y
22=8x
2,∴(y
1+y
2)(y
1-y
2)=8(x
1-x
2),∴
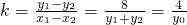
.
由N(x
0,y
0)在直线l上,∴
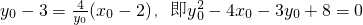
,
又当直线l斜率不存在时,直线方程为x=2,中点为(2,0)满足上述方程,
所以,所求中点N的轨迹方程为:y
2-4x-3y+8=0.
分析:(1)由题知l的斜率存在设斜率为且k≠0,根据
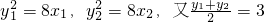
,可得
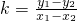
的值,点斜式求得AB所在直线l的方程.
(2)设AB的中点N(x
0,y
0 ),由中点公式及 y
12=8x
1,y
22=8x
2,求出l的斜率k=
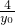
,再根据中点N(x
0,y
0)在直线l上,得到y
02-4x
0-3y
0+8=0,当直线l斜率不存在时,中点为(2,0)满足上述方程,从而得到中点N的轨迹方程为:y
2-4x-3y+8=0.
点评:本题考查直线和圆锥曲线的位置关系,轨迹方程的求法,体现了分类讨论的数学思想,求出直线的斜率,是
解题的关键.

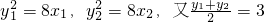 ,
,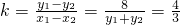 ,
, (x-2),即 4x-3y+1=0.
(x-2),即 4x-3y+1=0. 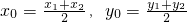 .
.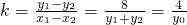 .
.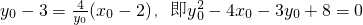 ,
,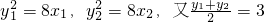 ,可得
,可得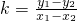 的值,点斜式求得AB所在直线l的方程.
的值,点斜式求得AB所在直线l的方程.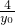 ,再根据中点N(x0,y0)在直线l上,得到y02-4x0-3y0+8=0,当直线l斜率不存在时,中点为(2,0)满足上述方程,从而得到中点N的轨迹方程为:y2-4x-3y+8=0.
,再根据中点N(x0,y0)在直线l上,得到y02-4x0-3y0+8=0,当直线l斜率不存在时,中点为(2,0)满足上述方程,从而得到中点N的轨迹方程为:y2-4x-3y+8=0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知抛物线y2=8x与椭圆
已知抛物线y2=8x与椭圆