练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知X和Y是两个分类变量，由公式K2= 算出K2的观测值k约为7.822根据下面的临界值表可推断（ ）

    P（K2≥k0）

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828


    A.推断“分类变量X和Y没有关系”犯错误的概率上界为0.010
    B.推断“分类变量X和Y有关系”犯错误的概率上界为0.010
    C.有至少99%的把握认为分类变量X和Y没有关系
    D.有至多99%的把握认为分类变量X和Y有关系

    【答案】A
    【解析】解：由K2= 算出K2的观测值k约为7.822，根据临界值表，
    由于7.86＞6.635，所以在犯错误的概率不超过0.01的前提下认为“分类变量X和Y没有关系”．
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的个数有（ ）
    ①函数f（x）=lg（2x﹣1）的值域为R；
    ②若（ ）a＞（ ）b ， 则a＜b；
    ③已知f（x）= ，则f[f（0）]=1；
    ④已知f（1）＜f（2）＜f（3）＜…＜f（2016），则f（x）在[1，2016]上是增函数．
    A.0个
    B.1个
    C.2 个
    D.3个Q

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知y=f（x）是定义在R上的奇函数，且x＞0时，f（x）=1+（ ）x
    （1）求函数f（x）的解析式；
    （2）画出函数f（x）的草图；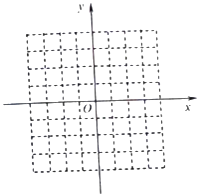

    （3）利用图象直接写出函数f（x）的单调区间及值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若变量x，y满足约束条件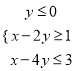 ，则z=3x+5y的取值范围是（　　）

    A. [3，+∞） B. [﹣8，3] C. （﹣∞，9] D. [﹣8，9]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， .

    (1)当 (为自然对数的底数)时，求曲线在点处的切线方程；

    (2)讨论函数的零点的个数；

    (3)若对任意， 恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图的程序框图表示求式子1×3×7×15×31×63的值，则判断框内可以填的条件为（ ）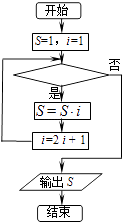

    A.i≤31？
    B.i≤63？
    C.i≥63？
    D.i≤127？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆心在轴上的圆过点和，圆的方程为.

    （1）求圆的方程；

    （2）由圆上的动点向圆作两条切线分别交轴于两点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知：2x≤256且log2x≥ ，
    （1）求x的取值范围；
    （2）求函数log2（ ）log2（ ）的最大值和最小值以及相应的x的取值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的广告费支出x与销售额y（单位：万元）之间有如表对应数据：

    x

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70


    （1）求广告费支出x与销售额y回归直线方程 =bx+a（a，b∈R）；
    已知b= ，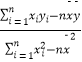
    （2）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．

    查看答案和解析>>

    同步练习册答案