
【题目】在等差数列{an}中,a14+a15+a16=﹣54,a9=﹣36,Sn为其前n项和.
(1)求Sn的最小值,并求出相应的n值;
(2)求Tn=|a1|+|a2|+…+|an|.
【答案】
(1)解:设等差数列{an}的公差为d,
∵a14+a15+a16=3a15=﹣54,a15=﹣18,
∴ ![]() ,
,
∴an=a9+(n﹣9)×d=3n﹣63,
∴an+1=3(n+1)﹣63=3n﹣60
令 ![]() ,
,
∴20≤n≤21,
∴ ![]() ,
,
即当n=20或21时,Sn最小且最小值为﹣630
(2)解:∵a1=﹣60,d=3,
∴an=﹣60+(n﹣1)×3=3n﹣63,
由an=3n﹣63≥0,得n≥21,
∵a20=3×20﹣63=﹣3<0,a21=3×21﹣63=0,
∴数列{an}中,前20项小于0,第21项等于0,以后各项均为正数,
当n≤21时, ![]()
当n≥22时, 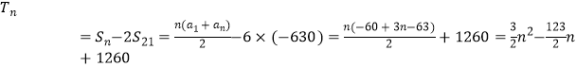
综上, 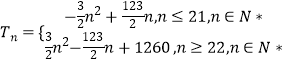
【解析】(1)由已知条件求出d=3,令 ![]() ,求出n的范围,求出Sn的最小值.(2)数列{an}中,前20项小于0,第21项等于0,以后各项均为正数,所以当n≤21时,Tn=﹣Sn , 当n>21时,Tn=Sn﹣2S21 , 由此利用分类讨论思想能求出Tn .
,求出n的范围,求出Sn的最小值.(2)数列{an}中,前20项小于0,第21项等于0,以后各项均为正数,所以当n≤21时,Tn=﹣Sn , 当n>21时,Tn=Sn﹣2S21 , 由此利用分类讨论思想能求出Tn .


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某校有学生2000人,其中高二学生630人,高三学生720人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高一学生的人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]()
(1)求函数f(x)的最小正周期和最大值,并求出x为何值时,f(x)取得最大值;
(2)求函数f(x)在[﹣2π,2π]上的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某大风车的半径为2m,每6s旋转一周,它的最低点O离地面0.5 m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m),则函数h=f(t)的关系式( )
A.y=﹣2cos![]() +2.5
+2.5
B.y=﹣2sin![]() +2.5
+2.5
C.y=﹣2cos![]() +2.5
+2.5
D.y=﹣2sin![]() +2.5
+2.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口的水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是每天时间与水深的关系表:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
经过长期观测,y=f(t)可近似的看成是函数y=Asinωt+b
(1)根据以上数据,求出y=f(t)的解析式;
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.
(1)将y表示为x的函数;
(2)试确定O点的位置,使铺设的排污管道的总长度最短,并求总长度的最短公里数(精确到0.01km).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项都是1的两个数列{an},{bn} ![]() 满足anbn+1﹣an+1bn﹣2an+1an=0.
满足anbn+1﹣an+1bn﹣2an+1an=0.
(1)令 ![]() ,求证数列{cn}为等差数列;
,求证数列{cn}为等差数列;
(2)若 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人射击一次命中7~10环的概率如下表
命中环数 | 7 | 8 | 9 | 10 |
命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com