解:(1)∵左焦点为F1(-

,0),
∴c
2=a
2-b
2=2,
∵椭圆过点M(

,1),
∴
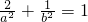
,
联立
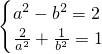
,得a
2=4,b
2=2,
∴椭圆C方程:

.
(2)存在经过定点(0,2)的直线l与椭圆C交于A、B两点并且满足

•
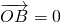
.
设直线l为y=kx+2,
把y=kx+2代入

,并整理,得(2k
2+1)x
2+8kx+4=0,
设A(x
1,y
1),B(x
2,y
2),
则
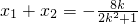
,
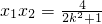
,
y
1y
2=(kx
1+2)(kx
2+2)=k
2x
1x
2+2k(x
1+x
2)+4=
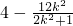
,
∵

,∴
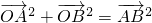
,
∴x
1x
2+y
1y
2=0,
∴

,
解得k=

,
∴直线l为
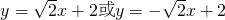
.
分析:(1)由左焦点为F1(-

,0),知c
2=a
2-b
2=2,由椭圆过点M(

,1),知
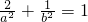
,联立
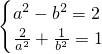
,能推导出椭圆C方程.
(2)设直线l为y=kx+2,把y=kx+2代入

,并整理,得(2k
2+1)x
2+8kx+4=0,设A(x
1,y
1),B(x
2,y
2),
则
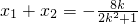
,
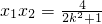
,y
1y
2=(kx
1+2)(kx
2+2)=k
2x
1x
2+2k(x
1+x
2)+4=
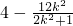
,由

,知x
1x
2+y
1y
2=0,所以

,由此能求出直线l的方程.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆、向量、韦达定理的相关知识,解题时要注意合理地进行等价转化.

 过点M(
过点M( ,1),且左焦点为
,1),且左焦点为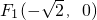 .
. •
•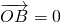 ,若存在求出直线l的方程,不存在说明理由.
,若存在求出直线l的方程,不存在说明理由. ,0),
,0), ,1),
,1),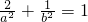 ,
,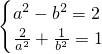 ,得a2=4,b2=2,
,得a2=4,b2=2, .
. •
•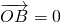 .
. ,并整理,得(2k2+1)x2+8kx+4=0,
,并整理,得(2k2+1)x2+8kx+4=0,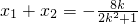 ,
,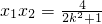 ,
,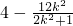 ,
, ,∴
,∴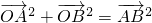 ,
, ,
, ,
,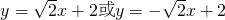 .
. ,0),知c2=a2-b2=2,由椭圆过点M(
,0),知c2=a2-b2=2,由椭圆过点M( ,1),知
,1),知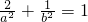 ,联立
,联立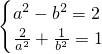 ,能推导出椭圆C方程.
,能推导出椭圆C方程. ,并整理,得(2k2+1)x2+8kx+4=0,设A(x1,y1),B(x2,y2),
,并整理,得(2k2+1)x2+8kx+4=0,设A(x1,y1),B(x2,y2),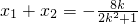 ,
,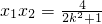 ,y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=
,y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=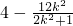 ,由
,由 ,知x1x2+y1y2=0,所以
,知x1x2+y1y2=0,所以 ,由此能求出直线l的方程.
,由此能求出直线l的方程.

 阅读快车系列答案
阅读快车系列答案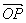 =
=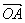 +
+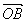 ),点N的坐标为(
),点N的坐标为(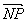 |的最小值与最大值.
|的最小值与最大值.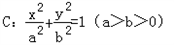 过点M(
过点M(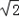 ,1),且左焦点为
,1),且左焦点为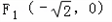 .
.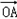 ·
·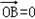 ,若存在求出直线l的方程,不存在说明理由.
,若存在求出直线l的方程,不存在说明理由.