
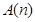 :
: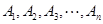 与
与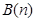 :
: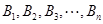 ,其中
,其中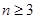 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段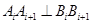 ,其中
,其中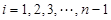 ,则称
,则称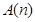 与
与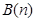 互为正交点列.
互为正交点列.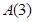 :
: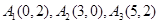 的正交点列
的正交点列 ;
;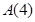 :
: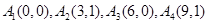 是否存在正交点列
是否存在正交点列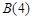 ?并说明理由;
?并说明理由;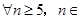 N,是否都存在无正交点列的有序整点列
N,是否都存在无正交点列的有序整点列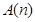 ?并证明你的结论.
?并证明你的结论.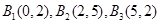 ,(2)不存在,(3)存在.
,(2)不存在,(3)存在. 与
与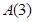 的起点和终点分别相同,所以
的起点和终点分别相同,所以 ,只需求
,只需求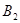 .由
.由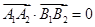 及
及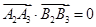 ,可解得
,可解得 本题实质考查对新定义的理解.关键逐条代入验证.(2)与(1)相似,从求
本题实质考查对新定义的理解.关键逐条代入验证.(2)与(1)相似,从求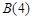 角度出发,能求出来就存在,否则就不存在.首先有
角度出发,能求出来就存在,否则就不存在.首先有 求
求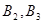 时,不是设四个未知数,二是利用向量垂直关系,设三个未知数,即
时,不是设四个未知数,二是利用向量垂直关系,设三个未知数,即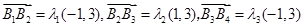 ,因为
,因为 相同,所以有
相同,所以有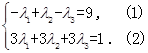 因为
因为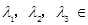
 ,所以方程组显然不成立,即不存在.
,所以方程组显然不成立,即不存在.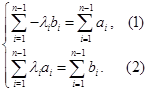 无解,须使得整数尽量取
无解,须使得整数尽量取 ,①当
,①当 为偶数时,取
为偶数时,取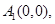
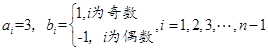 .②当
.②当 为奇数时,取
为奇数时,取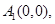
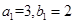 ,
,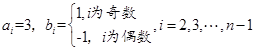 ,就可满足题意.
,就可满足题意.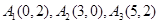 的正交点列是
的正交点列是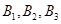 ,
, ,设
,设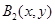 ,
,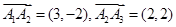 ,
,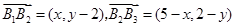 ,
,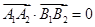 ,
,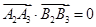 ,
,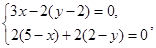 解得
解得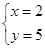
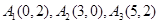 的正交点列是
的正交点列是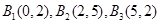 . 3分
. 3分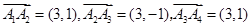 ,
,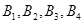 是点列
是点列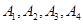 的正交点列,
的正交点列, ,
,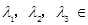

 相同,所以有
相同,所以有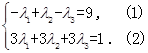
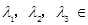
 ,方程(2)显然不成立,
,方程(2)显然不成立,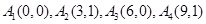 不存在正交点列; 8分
不存在正交点列; 8分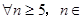
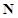 ,都存在整点列
,都存在整点列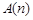 无正交点列. 9分
无正交点列. 9分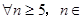
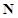 ,设
,设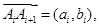 其中
其中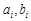 是一对互质整数,
是一对互质整数,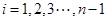
 是点列
是点列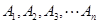 正交点列,
正交点列, ,
,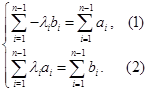
 为偶数时,取
为偶数时,取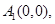
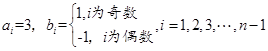 .
. 是整点列,所以有
是整点列,所以有
 ,
, .
.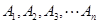 无正交点列;
无正交点列; 为奇数时,
为奇数时,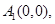
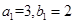 ,
,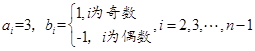 ,
, 是整点列,所以有
是整点列,所以有
 ,
, .
.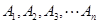 无正交点列.
无正交点列.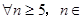
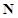 ,都不存在无正交点列的有序整数点列
,都不存在无正交点列的有序整数点列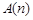 13分
13分

 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:不详 题型:填空题
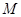 是梯形
是梯形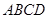 内或边界上的一个动点,点N是DC边的中点,则
内或边界上的一个动点,点N是DC边的中点,则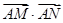 的最大值是________ .
的最大值是________ .
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ×
× )·
)·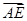 =( )
=( )
| A.4 | B.8 | C.2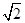 | D.4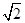 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com