
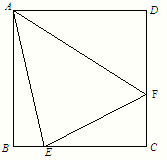
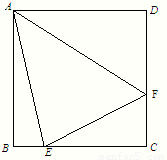
 如图,开发商欲对边长为1km的正方形ABCD地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路EF(点E、F分别在BC、CD上),根据规划要求△ECF的周长为2km.
如图,开发商欲对边长为1km的正方形ABCD地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路EF(点E、F分别在BC、CD上),根据规划要求△ECF的周长为2km.| x2+y2 |
| tanα+tanβ |
| 1-tanαtanβ |
| 2-(x+y) |
| x+y-xy |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| 1 |
| cosαcosβ |
| ||
| 4 |
| 1 | ||
cosαcos(
|
| 1 |
| sin2α+2cos2α |
| 1 | ||||
|
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
| π |
| 4 |
2tan
| ||
1-tan2
|
| π |
| 8 |
| 2 |
| 2 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年江苏省如东县高三12月四校联考文科数学试卷(解析版) 题型:解答题
(本题满分16分)
如图,开发商欲对边长为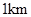 的正方形
的正方形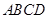 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路 (点
(点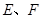 分别在
分别在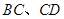 上),根据规划要求
上),根据规划要求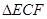 的周长为
的周长为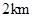 .
.

(1)设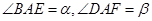 ,求证:
,求证: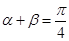 ;
;
(2)欲使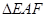 的面积最小,试确定点
的面积最小,试确定点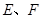 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三11月练习数学试卷 题型:解答题
如图,开发商欲对边长为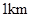 的正方形
的正方形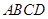 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路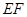 (点
(点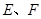 分别在
分别在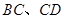 上),根据规划要求
上),根据规划要求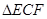 的周长为
的周长为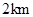 .
.

(1)设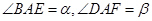 ,试求
,试求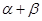 的大小;
的大小;
(2)欲使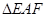 的面积最小,试确定点
的面积最小,试确定点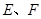 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市滨湖区梅村高级中学高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:《三角函数》2013年高三一轮复习单元训练(北京师范大学附中)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com