
 和
和 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
 元,
元, 长为
长为 米,试求
米,试求 关于
关于 的函数关系式;
的函数关系式; 为何值,
为何值, 取得最小值?并求出这个最小值.
取得最小值?并求出这个最小值. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题
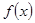 为n阶格点函数,已知函数:①
为n阶格点函数,已知函数:①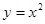 ;②
;②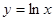 ;③
;③ ;④
;④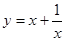 ;⑤
;⑤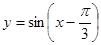 ;⑥
;⑥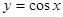 .其中为一阶格点函数的序号为
.其中为一阶格点函数的序号为 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为 ,已知此生产线年产量最大为210吨。
,已知此生产线年产量最大为210吨。 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;②
;② ;③
;③ .(以上三式中、
.(以上三式中、 均为常数,且
均为常数,且 )
) ,
, ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是 .其中
.其中 表示8月1日,
表示8月1日, 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
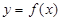 为“
为“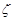 函数”:存在一条与函数
函数”:存在一条与函数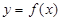 的图象有两个不同交点(设为
的图象有两个不同交点(设为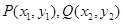 )的直线,
)的直线, 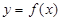 在
在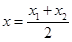 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数: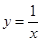 ②
②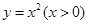 ③
③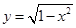 ④
④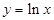 ,
,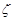 函数”的是 (将所有你认为正确的序号填在横线上)
函数”的是 (将所有你认为正确的序号填在横线上)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 满足下列三个条件
满足下列三个条件 都有
都有 ;
; 都有
都有 ;
; 的图像关于
的图像关于 轴对称.
轴对称.A. | B. |
C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com