
����Ŀ��ijѧУΪ���˽�ѧ��ʹ���ֻ���������ֱ��ڸ�һ�߶������꼶�������ȡ��100��ѧ�����е���.�����Ǹ��ݵ��������Ƶ�ѧ���վ�ʹ���ֻ�ʱ���Ƶ���ֲ�����Ƶ�ʷֲ�ֱ��ͼ����ʹ���ֻ�ʱ�䲻����80���ӵ�ѧ����Ϊ���ֻ��ԡ�.
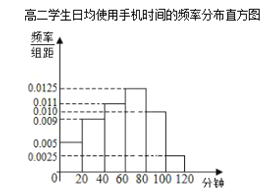
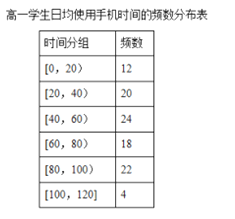
��I����Ƶ����Ϊ���ʣ������ĸ��꼶��ѧ���ǡ��ֻ��ԡ��ĸ��ʴ���˵������.
��II���ڸ߶��ij���У���֪����鵽��Ů������55��������10��Ϊ���ֻ��ԡ�.������֪������������2��2�����������ݴ��������ж��İ�����Ϊ���ֻ��ԡ����Ա��йأ�
���ֻ��� | �ֻ��� | �ϼ� | |
�� | |||
Ů | |||
�ϼ� |
�����������![]() ������
������![]() ����������.
����������.
����� |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
���𰸡�����һ�꼶�����ɼ�������������������������90%
��������
������Ƶ���ֲ�����Ƶ�ʷֲ�ֱ��ͼ���ֱ���������꼶ѧ���ǡ��ֻ��ԡ��ĸ��ʣ����ɱȽϣ������ж�.
���������⣬����ֻ��������ͷ��ֻ��������������������������ɶ����Լ���Ĺ�ʽ���![]() �����������жϼ���.
�����������жϼ���.
������Ƶ���ֲ�����֪����һѧ���ǡ��ֻ��ԡ��ĸ���Ϊ![]()
��Ƶ�ʷֲ�ֱ��ͼ��֪���߶�ѧ���ǡ��ֻ��ԡ��ĸ���Ϊ![]() =��0.0025+0.010����20=0.25
=��0.0025+0.010����20=0.25
��ΪP1![]() P2�����Ը�һ�꼶��ѧ���ǡ��ֻ��ԡ��ĸ��ʴ�.
P2�����Ը�һ�꼶��ѧ���ǡ��ֻ��ԡ��ĸ��ʴ�.
������Ƶ�ʷֲ�ֱ��ͼ��֪���ڳ�ȡ��100���У�
���ֻ��ԡ��У�0.010+0.0025����20��100=25���ˣ���
���ֻ�����100��25=75���ˣ�.
�Ӷ�2��2���������£�
���ֻ��� | �ֻ��� | �ϼ� | |
�� | 30 | 15 | 45 |
Ů | 45 | 10 | 55 |
�ϼ� | 75 | 25 | 100 |
��2��2�������е����ݴ��빫ʽ���㣬
��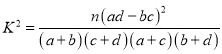
![]()
��ϲο����ݣ���֪3.030![]() 2.706��������90%�İ�����Ϊ���ֻ��ԡ����Ա��й�.
2.706��������90%�İ�����Ϊ���ֻ��ԡ����Ա��й�.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=mx2+��1-3m��x-4��m��R��
��1����m=1ʱ����f��x��������[-2��2]�ϵ����ֵ����Сֵ��
��2�������x�IJ���ʽf��x����-1��
��3����m��0ʱ��������x0�ʣ�1��+�ޣ���ʹ��f��x����0����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ���������ں�ָ���Ǻ�������ý�����й�������Ӱ�������ۺ�ָ�꣬������ر����ṩ��ȫ������2018��ijȫ���Դ��ͻ����ʡ����������̨���ں�ָ�������ݣ�������ǰ20������ʡ����������̨�����ں�ָ�����з���ͳ�ƣ���������ʾ.
��� | ���� | Ƶ�� |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
�ִ��ں�ָ����![]() ��
��![]() �ڵ���ʡ����������̨���������ȡ2�ҽ��е��У���������1�ҵ��ں�ָ����
�ڵ���ʡ����������̨���������ȡ2�ҽ��е��У���������1�ҵ��ں�ָ����![]() �ڵĸ���.
�ڵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l�IJ�������Ϊ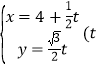 Ϊ����
Ϊ����![]() ��������ԭ��Ϊ���㣬x���������Ϊ���Ὠ����������ϵ������C�ļ����귽��Ϊ
��������ԭ��Ϊ���㣬x���������Ϊ���Ὠ����������ϵ������C�ļ����귽��Ϊ![]() ��
��
![]() ������C��ֱ�����귽����ֱ��l�ļ����귽�̣�
������C��ֱ�����귽����ֱ��l�ļ����귽�̣�
![]() ��
��![]() ��ֱ��
��ֱ��![]() ������C���ڵ�
������C���ڵ�![]() ��ͬ��ԭ��
��ͬ��ԭ��![]() ����ֱ��l���ڵ�B����
����ֱ��l���ڵ�B����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ǣ���ֱ��ƽ����ƽ�棬��ƽ����ƽ���ڵ�����ֱ�ߣ���ֱ֪��![]() ƽ��
ƽ��![]() ��ֱ��
��ֱ��![]() ƽ��
ƽ��![]() ��ֱ��
��ֱ��![]() ƽ��
ƽ��![]() ����ֱ��
����ֱ��![]() ƽ��
ƽ��![]() .���������Ȼ�Ǵ���ģ�������Ϊ �� ��
.���������Ȼ�Ǵ���ģ�������Ϊ �� ��
A.ʹ��������������������ǰ���Ǵ����B.ʹ������������������Сǰ���Ǵ����
C.ʹ���˹�������D.ʹ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������2013-2017��������������Ѫѹֵ������ͼ��ͼ��ʾ.
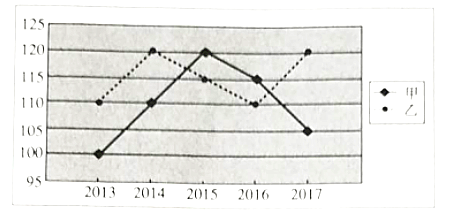
��1������ɢ��ͼ��ֱ���жϼס����������������Ѫѹֵ˭�IJ��������������ߵķ��
��2��������������������Ѫѹֵ�����ݣ���������Ѫѹֵ![]() �������
�������![]() �����Իع鷽�̣����ݴ˹�������2018���������Ѫѹֵ.
�����Իع鷽�̣����ݴ˹�������2018���������Ѫѹֵ.
������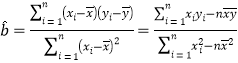 ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���![]() ������ʵ��
������ʵ��![]() ������
������![]() ���ҵ�
���ҵ�![]() ʱ��
ʱ��![]() ��
��
��1���жϺ���![]() ����ż�ԣ���֤����
����ż�ԣ���֤����
��2���жϺ���![]() �ĵ����ԣ���֤����
�ĵ����ԣ���֤����
��3���ⲻ��ʽ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020������ҹ�ͻ���¹ڷ�������.��ԡ�ͻ�����ѡ����ٹ������ģ��̽�ž�ҽ�ƶ��ڳ�Ϧҹ�ɵ��人����ʡҽ�ƶ�Ҳ½����Ԯ����Ͷ����������벡�˾���֮��.Ϊ�ֵ��������ߡ��ĺ��֮�ǣ�ij��ѧѧ��־Ը���Ŷӿ�չ�����ĸ�ѧ�����Ϊ����ǰ�߹�������Ů���߸�������.��������żס��ҡ���3��־Ը��Ϊijѧ��������ѧ����������ѧ������4��ѧ�ƣ�ÿ��־Ը�����ٸ���1��ѧ�ƣ�ÿ��ѧ����1��־Ը�߸���������ѧѧ��ǡ���ɼ����ĸ���Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCDEF�У��ı���ABCDΪ���Σ������A-CD-FΪ60�㣬DE��CF��CD��DE��AD=2��DE=DC=3��CF=6.

��1����֤��BF��ƽ��ADE��
��2�����߶�CF����һ��G��ʹ������B-EG-D������ֵΪ![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com