
【题目】如图,多面体ABCDEF中,四边形ABCD为矩形,二面角A-CD-F为60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=6.

(1)求证:BF∥平面ADE;
(2)在线段CF上求一点G,使锐二面角B-EG-D的余弦值为![]() .
.
【答案】(1)详见解析;(2)点![]() 满足
满足![]() .
.
【解析】
(1)先证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可得平面
,可得平面![]() 平面
平面![]() ,从而可得结果;(2)作
,从而可得结果;(2)作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,以平行于
,以平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,利用向量垂直数量积为零列方程组求得平面
,利用向量垂直数量积为零列方程组求得平面![]() 的法向量,结合面
的法向量,结合面![]() 的一个法向量为
的一个法向量为![]() ,利用空间向量夹角余弦公式列方程解得
,利用空间向量夹角余弦公式列方程解得![]() ,从而可得结果.
,从而可得结果.
(1)因为ABCD是矩形,所以BC∥AD,
又因为BC不包含于平面ADE,
所以BC∥平面ADE,
因为DE∥CF,CF不包含于平面ADE,
所以CF∥平面ADE,
又因为BC∩CF=C,所以平面BCF∥平面ADF,
而BF平面BCF,所以BF∥平面ADE.
(2)∵CD⊥AD,CD⊥DE
∴∠ADE为二面角A-CD-F的平面角
∴∠ADE=60°
∵CD⊥面ADE
![]() 平面
平面![]() 平面
平面![]() ,作
,作![]() 于点
于点![]() ,
,
则![]() 平面
平面![]() ,
,
由![]() ,得
,得![]() ,
,
以![]() 为原点,平行于
为原点,平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,
建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则由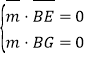 ,得
,得![]() ,取
,取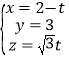 ,
,
得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又面![]() 的一个法向量为
的一个法向量为![]() ,
,
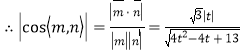 ,
,
![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
此时![]() ,得
,得![]() ,
,
即所求线段![]() 上的点
上的点![]() 满足
满足![]() .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】如图(示意),公路AM、AN围成的是一块顶角为钝角α的角形耕地,其中![]() .在该块土地中
.在该块土地中![]() 处有一小型建筑,经测量,它到公路
处有一小型建筑,经测量,它到公路![]() 、
、![]() 的距离
的距离![]() 、
、![]() 分别为
分别为![]() ,
,![]() .现要过点
.现要过点![]() 修建一条直线公路
修建一条直线公路![]() ,将三条公路围成的区域
,将三条公路围成的区域![]() 建成一个工业园.设
建成一个工业园.设![]() ,
,![]()
![]() ,其中
,其中![]() .
.

(1)试建立![]() 间的等量关系;
间的等量关系;
(2)为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,等腰梯形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起后如图2,使二面角
折起后如图2,使二面角![]() 成直二面角,设
成直二面角,设![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 的中
的中
点.
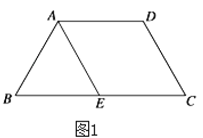

(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)判断![]() 能否垂直于平面
能否垂直于平面![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将给定的一个数列![]() :
:![]() ,
,![]() ,
,![]() ,…按照一定的规则依顺序用括号将它分组,则可以得到以组为单位的序列.如在上述数列中,我们将
,…按照一定的规则依顺序用括号将它分组,则可以得到以组为单位的序列.如在上述数列中,我们将![]() 作为第一组,将
作为第一组,将![]() ,
,![]() 作为第二组,将
作为第二组,将![]() ,
,![]() ,
,![]() 作为第三组,…,依次类推,第
作为第三组,…,依次类推,第![]() 组有
组有![]() 个元素(
个元素(![]() ),即可得到以组为单位的序列:
),即可得到以组为单位的序列:![]() ,
,![]() ,
,![]() ,…,我们通常称此数列为分群数列.其中第1个括号称为第1群,第2个括号称为第2群,第3个数列称为第3群,…,第
,…,我们通常称此数列为分群数列.其中第1个括号称为第1群,第2个括号称为第2群,第3个数列称为第3群,…,第![]() 个括号称为第
个括号称为第![]() 群,从而数列
群,从而数列![]() 称为这个分群数列的原数列.如果某一个元素在分群数列的第
称为这个分群数列的原数列.如果某一个元素在分群数列的第![]() 个群众,且从第
个群众,且从第![]() 个括号的左端起是第
个括号的左端起是第![]() 个,则称这个元素为第
个,则称这个元素为第![]() 群众的第
群众的第![]() 个元素.已知数列1,1,3,1,3,9,1,3,9,27,…,将数列分群,其中,第1群为(1),第2群为(1,3),第3群为(1,3,
个元素.已知数列1,1,3,1,3,9,1,3,9,27,…,将数列分群,其中,第1群为(1),第2群为(1,3),第3群为(1,3,![]() ),…,以此类推.设该数列前
),…,以此类推.设该数列前![]() 项和
项和![]() ,若使得
,若使得![]() 成立的最小
成立的最小![]() 位于第
位于第![]() 个群,则
个群,则![]() ( )
( )
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0,则称x0是f(x)的一个不动点,已知f(x)=x2+ax+4在[1,3]恒有两个不同的不动点,则实数a的取值范围______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民营企业生产A,B两种产品,根据市场调查与预测,A产品的利润y与投资x成正比,其关系如图甲,B产品的利润y与投资x的算术平方根成正比,其关系如图乙![]() 注:利润与投资单位为万元
注:利润与投资单位为万元![]()
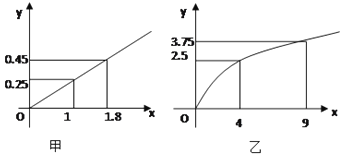
![]() 分别将A,B两种产品的利润y表示为投资x的函数关系式;
分别将A,B两种产品的利润y表示为投资x的函数关系式;
![]() 该企业已筹集到10万元资金,并全部投入A,B两种产品的生产
该企业已筹集到10万元资金,并全部投入A,B两种产品的生产![]() 问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com