
已知函数f(x)=ax3+bx2经过点M(1,4),在点M处的切线恰与直线x+9y+5=0垂直.
(1)求a,b的值;
(2)若函数f(x)在区间[m-1,m+1]上单调递增,求实数m的取值范围.
科目:高中数学 来源: 题型:
预计某地区明年从年初开始的前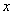 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量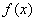 (万件)近似满足:
(万件)近似满足: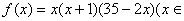 N*,且
N*,且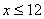 )
)
(1)写出明年第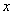 个月的需求量
个月的需求量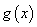 (万件)与月份
(万件)与月份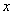 的函数关系式,并求出哪个月份的需求量超过
的函数关系式,并求出哪个月份的需求量超过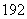 万件;
万件;
(2)如果将该商品每月都投放到该地区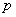 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应,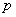 应至少为多少万件?(积压商品转入下月继续销售)
应至少为多少万件?(积压商品转入下月继续销售)
查看答案和解析>>
科目:高中数学 来源: 题型:
直线L: 与椭圆C:
与椭圆C: 交于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交于A、B两点,以OA、OB为邻边作平行四边形OAPB。
求证:椭圆C: 与直线L:
与直线L: 总有两个交点。当
总有两个交点。当 时,求点P的轨迹方程。
时,求点P的轨迹方程。
(3)是否存在直线L,使OAPB为矩形?若存在,求出此时直线L的方程;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com