已知集合A={(x,y)|x-y+m≥0},集合B={(x,y)|x2+y2≤1}.若A∩B=φ,则实数m的取值范围是 ________.
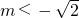
分析:利用集合A中的点构成平面区域与集合B构成的圆面无公共部分,数学结合判断出直线与圆的关系是相离.利用圆心到直线的距离大于半径求出m的范围.
解答:

解:如图,A={(x,y)|x-y+m≥0}表示直线x-y+m=0及其下方区域,
B={(x,y)|x
2+y
2≤1}表示圆x
2+y
2=1及内部,
要使A∩B=φ,则直线x-y+m=0在圆x
2+y
2=1的下方,
即
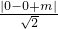
>1,故
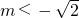
.
故答案为:
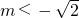
.
点评:本题考查将集合的关系转化成图形的关系;直线与圆的位置关系;点到直线的距离公式.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案