
【题目】已知椭圆![]() 的左焦点为F,短轴的两个端点分别为A,B,且
的左焦点为F,短轴的两个端点分别为A,B,且![]() ,
,![]() 为等边三角形.
为等边三角形.

(1)求椭圆C的方程;
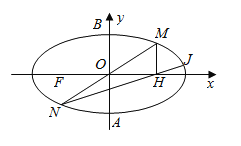
(2)如图,点M在椭圆C上且位于第一象限内,它关于坐标原点O的对称点为N;过点M作x轴的垂线,垂足为H,直线![]() 与椭圆C交于另一点J,若
与椭圆C交于另一点J,若![]() ,试求以线段
,试求以线段![]() 为直径的圆的方程;
为直径的圆的方程;
(3)已知![]() 是过点A的两条互相垂直的直线,直线
是过点A的两条互相垂直的直线,直线![]() 与圆
与圆![]() 相交于P,Q两点,直线
相交于P,Q两点,直线![]() 与椭圆C交于另一点R,求
与椭圆C交于另一点R,求![]() 面积最大值时,直线
面积最大值时,直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)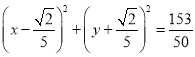 (3)
(3)![]()
【解析】
(1)由题意可得![]() ,
,![]() ,由
,由![]() ,
,![]() ,
,![]() 的关系,可得
的关系,可得![]() 的值,进而得椭圆
的值,进而得椭圆![]() 方程;
方程;
(2)设![]() ,即有
,即有![]() ,
,![]() ,
,![]() ,运用向量的数量积的坐标表示,可得
,运用向量的数量积的坐标表示,可得![]() ,
,![]() ,求出
,求出![]() 的方程,代入椭圆方程,可得
的方程,代入椭圆方程,可得![]() 的坐标,求得
的坐标,求得![]() 的中点坐标和半径,进而可得圆的方程;
的中点坐标和半径,进而可得圆的方程;
(3)设![]() ,代入椭圆方程可得,运用韦达定理和弦长公式,再由三角形的面积公式,运用配方和二次函数的最值得求法,即可得到所求直线的方程.
,代入椭圆方程可得,运用韦达定理和弦长公式,再由三角形的面积公式,运用配方和二次函数的最值得求法,即可得到所求直线的方程.
(1)由题意可得![]() ,即
,即![]() ,又
,又![]() 为等边三角形,可得
为等边三角形,可得![]() ,
,
所以![]() ,
,
所以,椭圆![]() 的方程为:
的方程为:![]() .
.
(2)设![]() ,即有
,即有![]() ,
,![]() ,
,![]() ,
,
由题意得,![]() ,即为
,即为![]() ,解得
,解得![]() ,
,
代入椭圆方程可得,![]() ,解得
,解得![]() ,即有
,即有 ,
,![]() ,
,
所以直线![]() 方程为:
方程为:![]() ,将其代入椭圆方程得:
,将其代入椭圆方程得:![]() ,
,
由![]() ,解得
,解得![]() 点坐标为
点坐标为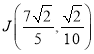 ,则
,则![]() 中点为
中点为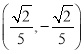 ,
,
所以圆的半径为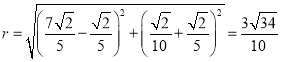 ,
,
即以线段![]() 为直径的圆的方程为:
为直径的圆的方程为: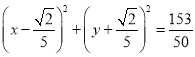 .
.
(3)设![]() ,代入椭圆方程可得,
,代入椭圆方程可得,![]() ,
,
解得![]() ,
,![]() ,则
,则 ,
,
由题意可得直线![]() 的方程为
的方程为![]() ,代入圆的方程
,代入圆的方程![]() 中,
中,
由弦长公式可得 ,
,
则![]() 的面积为
的面积为

令![]() ,即有
,即有![]() ,
,
所以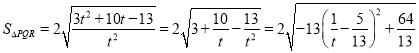
所以当![]() ,即有
,即有![]() ,此时
,此时![]() ,
,![]() 有最大值,
有最大值,
即有直线![]() 的方程为
的方程为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在2019年女排世界杯中,中国女子排球队以11连胜的优异战绩成功夺冠,为祖国母亲七十华诞献上了一份厚礼.排球比赛采用5局3胜制,前4局比赛采用25分制,每个队只有赢得至少25分,并同时超过对方2分时,才胜1局;在决胜局(第五局)采用15分制,每个队只有赢得至少15分,并领先对方2分为胜.在每局比赛中,发球方赢得此球后可得1分,并获得下一球的发球权,否则交换发球权,并且对方得1分.现有甲乙两队进行排球比赛:
(1)若前三局比赛中甲已经赢两局,乙赢一局.接下来两队赢得每局比赛的概率均为![]() ,求甲队最后赢得整场比赛的概率;
,求甲队最后赢得整场比赛的概率;
(2)若前四局比赛中甲、乙两队已经各赢两局比赛.在决胜局(第五局)中,两队当前的得分为甲、乙各14分,且甲已获得下一发球权.若甲发球时甲赢1分的概率为![]() ,乙发球时甲赢1分的概率为
,乙发球时甲赢1分的概率为![]() ,得分者获得下一个球的发球权.设两队打了
,得分者获得下一个球的发球权.设两队打了![]() 个球后甲赢得整场比赛,求x的取值及相应的概率p(x).
个球后甲赢得整场比赛,求x的取值及相应的概率p(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 且侧棱
且侧棱![]() 其中
其中![]() 为
为![]() 的
的![]() 交点.
交点.
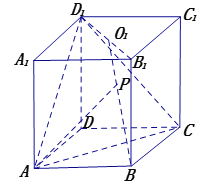
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)在线段![]() 上,是否存在一个点
上,是否存在一个点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直?若存在,求出线段
垂直?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合![]() 是由一些函数组成,满足如下性质:①对任意
是由一些函数组成,满足如下性质:①对任意![]() ,
,![]() 均存在反函数
均存在反函数![]() ,且
,且![]() ;②对任意
;②对任意![]() ,方程
,方程![]() 均有解;③对任意
均有解;③对任意![]() 、
、![]() ,若函数
,若函数![]() 为定义在
为定义在![]() 上的一次函数,则
上的一次函数,则![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求证:函数
中,求证:函数![]() ;
;
(2)若函数![]() (
(![]() )在集合
)在集合![]() 中,求实数
中,求实数![]() 的取值范围;
的取值范围;
(3)若集合![]() 中的函数均为定义在
中的函数均为定义在![]() 上的一次函数,求证:存在一个实数
上的一次函数,求证:存在一个实数![]() ,使得对一切
,使得对一切![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1260 m,经测量,cos A=![]() ,cos C=
,cos C=![]()
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量![]() ,两组向量
,两组向量![]() 和
和![]() 均由2个
均由2个![]() 和3个
和3个![]() 排列而成,记
排列而成,记![]() ,
,![]() 表示
表示![]() 所有可能取值中的最小值,则下列命题中
所有可能取值中的最小值,则下列命题中
(1)![]() 有5个不同的值;(2)若
有5个不同的值;(2)若![]() 则
则![]() 与
与![]() 无关;(3)若
无关;(3)若![]() ,则
,则![]() 与
与![]() 无关;(4)若
无关;(4)若![]() ,则
,则![]() ;(5)若
;(5)若![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() .正确的是( )
.正确的是( )
A.(1)(2)B.(2)(4)C.(3)(5)D.(1)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com