
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,记
时,记![]() 在区间
在区间![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见详解;(2) ![]() .
.
【解析】
(1)先求![]() 的导数,再根据
的导数,再根据![]() 的范围分情况讨论函数单调性;(2) 讨论
的范围分情况讨论函数单调性;(2) 讨论![]() 的范围,利用函数单调性进行最大值和最小值的判断,最终求得
的范围,利用函数单调性进行最大值和最小值的判断,最终求得![]() 的取值范围.
的取值范围.
(1)对![]() 求导得
求导得![]() .所以有
.所以有
当![]() 时,
时,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增;
区间上单调递增;
当![]() 时,
时,![]() 区间上单调递增;
区间上单调递增;
当![]() 时,
时,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增.
区间上单调递增.
(2)
若![]() ,
,![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,所以区间
单调递增,所以区间![]() 上最小值为
上最小值为![]() .而
.而![]() ,故所以区间
,故所以区间![]() 上最大值为
上最大值为![]() .
.
所以![]() ,设函数
,设函数![]() ,求导
,求导![]() 当
当![]() 时
时![]() 从而
从而![]() 单调递减.而
单调递减.而![]() ,所以
,所以![]() .即
.即![]() 的取值范围是
的取值范围是![]() .
.
若![]() ,
,![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,所以区间
单调递增,所以区间![]() 上最小值为
上最小值为![]() 而
而![]() ,故所以区间
,故所以区间![]() 上最大值为
上最大值为![]() .
.
所以![]() ,而
,而![]() ,所以
,所以![]() .即
.即![]() 的取值范围是
的取值范围是![]() .
.
综上得![]() 的取值范围是
的取值范围是![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,短轴的两个端点分别为A,B,且
的左焦点为F,短轴的两个端点分别为A,B,且![]() ,
,![]() 为等边三角形.
为等边三角形.

(1)求椭圆C的方程;
(2)如图,点M在椭圆C上且位于第一象限内,它关于坐标原点O的对称点为N;过点M作x轴的垂线,垂足为H,直线![]() 与椭圆C交于另一点J,若
与椭圆C交于另一点J,若![]() ,试求以线段
,试求以线段![]() 为直径的圆的方程;
为直径的圆的方程;
(3)已知![]() 是过点A的两条互相垂直的直线,直线
是过点A的两条互相垂直的直线,直线![]() 与圆
与圆![]() 相交于P,Q两点,直线
相交于P,Q两点,直线![]() 与椭圆C交于另一点R,求
与椭圆C交于另一点R,求![]() 面积最大值时,直线
面积最大值时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 和函数
和函数![]() ,
,
(1)若![]() 为偶函数,试判断
为偶函数,试判断![]() 的奇偶性;
的奇偶性;
(2)若方程![]() 有两个不等的实根
有两个不等的实根![]() ,则
,则
①试判断函数![]() 在区间
在区间![]() 上是否具有单调性,并说明理由;
上是否具有单调性,并说明理由;
②若方程![]() 的两实根为
的两实根为![]() 求使
求使![]() 成立的
成立的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至2019年10月27日在中国武汉举行,第七届世界军人运动会是我国第一次承办的综合性国际军事体育赛事,也是继北京奥运会之后我国举办的规模最大的国际体育盛会.来自109个国家的9300余名军体健儿在江城武汉同场竞技、增进友谊.运动会共设置射击、游泳、田径、篮球等27个大项、329个小项.经过激烈角逐,奖牌榜的前6名如下:
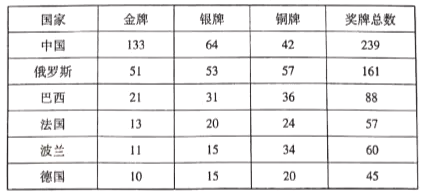
某大学德语系同学利用分层抽样的方式从德国获奖选手中抽取了9名获奖代表.
(1)请问这9名获奖代表中获金牌、银牌、铜牌的人数分别是多少人?
(2)从这9人中随机抽取3人,记这3人中银牌选手的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)从这9人中随机抽取3人,求已知这3人中有获金牌运动员的前提下,这3人中恰好有1人为获铜牌运动员的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的内切圆与三边
的内切圆与三边![]() 的切点分别为
的切点分别为![]() ,已知
,已知![]() ,内切圆圆心
,内切圆圆心![]() ,设点A的轨迹为R.
,设点A的轨迹为R.
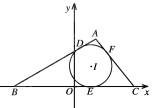
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使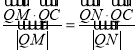 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
![]()
根据以上数据,绘制了散点图.
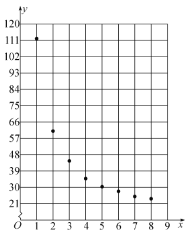
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() .参考数据(其中
.参考数据(其中![]() ):
):

(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: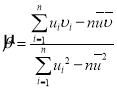 ,
,![]() ,相关系数
,相关系数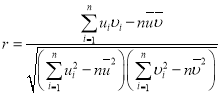 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com