【题目】已知某几何体的三视图如图所示，则它的外接球表面积为________．
【答案】4π
【解析】由三视图可知该几何体是三棱锥，且三棱锥的高为1，底面为一个直角三角形，由于底面斜边上的中线长为1，则底面的外接圆半径为1，顶点在底面上的投影落在底面外接圆的圆心上，由于顶点到底面的距离与底面外接圆的半径相等，则三棱锥的外接球半径R为1，则三棱锥的外接球表面积S＝4πR2＝4π.
点睛:空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．
(2)若球面上四点
构成的三条线段
两两互相垂直，且
，一般把有关元素“补形”成为一个球内接长方体，利用
求解．
科目：高中数学 来源： 题型：
【题目】某城市
户居民的月平均用电量（单位：度），以
，
，
，
，
，
，
分组的频率分布直方图如图．
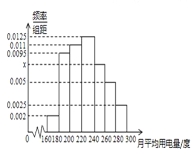
（I）求直方图中
的值；
（II）求月平均用电量的众数和中位数；
（III）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取
户居民，则月平均用电量在的用户中应抽取多少户？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在边长为1的等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图2所示的三棱锥A﹣BCF，其中BC=
．
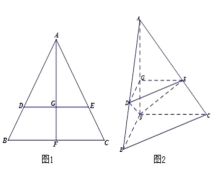
（Ⅰ）证明：DE∥平面BCF；
（Ⅱ）证明：CF⊥平面ABF；
（Ⅲ）当AD=
时，求三棱锥F﹣DEG的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
(1)化
的方程为普通方程，并说明它们分别表示什么曲线；
(2)若
上的点P对应的参数为
，Q为
上的动点，求PQ的中点M到直线
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知国家某5A级大型景区对拥挤等级与每日游客数量
（单位：百人）的关系有如下规定：当
时，拥挤等级为“优”；当
时，拥挤等级为“良”；当
时，拥挤等级为“拥挤”；当
时，拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据：
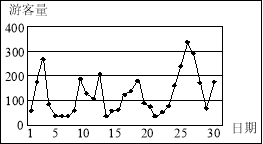
（Ⅰ）下面是根据统计数据得到的频率分布表，求出
的值，并估计该景区6月份游客人数的平均值（同一组中的数据用该组区间的中点值作代表）；
游客数量 （单位：百人） |
|
|
|
|
天数 |
|
|
|
|
频率 |
|
|
|
|
（Ⅱ）某人选择在6月1日至6月5日这5天中任选2天到该景区游玩，求他这2天遇到的游客拥挤等级均为“优”的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知过点
的直线
的参数方程是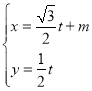
（
为参数）．以平面直角坐标系的原点为极点，
轴的正半轴为极轴，建立极坐标系，曲线
的极坐标方程式为
.
（Ⅰ）求直线的普通方程和曲线
的直角坐标方程；
（Ⅱ）若直线与曲线
交于两点
，且
，求实数
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心在坐标原点
的椭圆
经过点
，且点
为其右焦点.
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）是否存在平行于
的直线
，使得直线与椭圆
有公共点，且直线与的距离等于4？若存在，求出直线的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】通常表明地震能量大小的尺度是里氏震级，其计算公式为：
，其中，
是被测地震的最大振幅，
是“标准地震”的振幅（使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差）。
（1）假设在一次地震中，一个距离震中100千米的测震仪记录的地震最大振幅是30，此时标准地震的振幅是0．001，计算这次地震的震级（精确到0．1）；
（2）5级地震给人的震感已比较明显，计算8级地震的最大振幅是5级地震的最大振幅的多少倍？
（以下数据供参考：
， 
）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
