
【题目】设全集U=R,集合A={x|y=![]() },B={x|x2-x-6=0}.
},B={x|x2-x-6=0}.
(1)若a=-1,求A∩B;
(2)若(![]() )∩B=,求实数a的取值范围.
)∩B=,求实数a的取值范围.
【答案】(1) {-2};(2) (3,+∞).
【解析】试题分析:(1) 先求出集合B={-2,3},又a-x>0,解得集合A=(-∞,a),将a=-1代入,求出集合的交集;(2)先求出集合A的补集,根据(![]() )∩B=,求出a的范围.
)∩B=,求出a的范围.
试题解析:
(1)∵x2-x-6=0,
∴x1=3或x2=-2
∴B={-2,3}
∵a-x>0
∴x<a
∴A=(-∞,a)
∵a=-1,∴A=(-∞,-1)
∴A∩B={-2}
(2)∵![]() A=[a,+∞),B={-2,3},(
A=[a,+∞),B={-2,3},(![]() A)∩B=
A)∩B=
∴a>3,即a∈(3,+∞).
点睛: 1.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其他的集合.2.求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解.3.在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为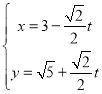 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com