
如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.

(1)求证:BC∥l.
(2)MN与平面PAD是否平行,试证明你的结论.
|
解:(1)∵四边形ABCD是平行四边形,∴BC∥AD. 又∵AD BC∥平面PAD. 又∵平面PBC∩平面PAD=l,BC (2)MN∥平面PAD. 证明:取PD的中点E,连结AE、NE. ∵NE ∴NE ∴MN∥AE.∵AE 思路解析:(1)按线面平行的判定和性质; (2)MN与平面PAD是否平行,看能否在平面PAD中,找到一条直线平行于MN.一般的思路是“给中点,再找中点”,即选取PD的中点E,连结AE、NE,则从四边形MNEA中可求得. |


科目:高中数学 来源: 题型:
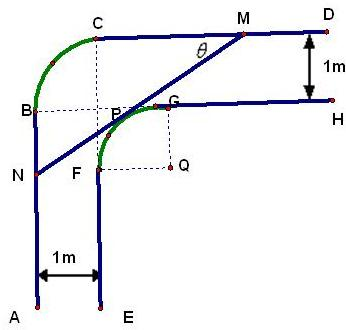 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.查看答案和解析>>
科目:高中数学 来源:福建省福州市2012届高三综合练习数学文科试题 题型:044
已知四棱锥P-ABCD的三视图如图所示,△PBC为正三角形.
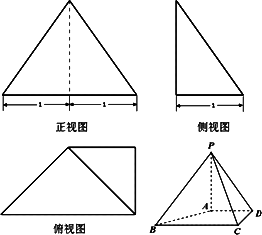
(Ⅰ)在平面PCD中作一条与底面ABCD平行的直线,并说明理由;
(Ⅱ)求证:AC⊥平面PAB;
(Ⅲ)求三棱锥A-PBC的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
若水平放置的木棒MN的两个端点M、N分别在外壁CD和AB上,且木棒与内壁圆弧相切于点P。设![]() ,试用
,试用![]() 表示木棒MN和长度
表示木棒MN和长度![]() 。
。
若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)
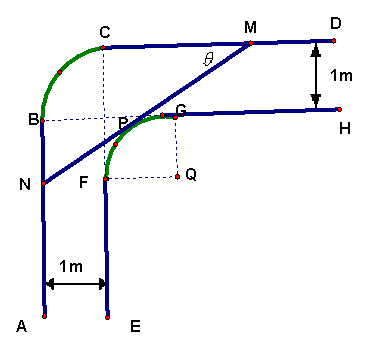
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
若水平放置的木棒MN的两个端点M、N分别在外壁CD和AB上,且木棒与内壁圆弧相切于点P。设![]() ,试用
,试用![]() 表示木棒MN和长度
表示木棒MN和长度![]() 。
。
若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值。

查看答案和解析>>
科目:高中数学 来源: 题型:
过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有( )
A.4条 B.6条
C.8条 D.12条
[答案] D
[解析] 如图所示,设M、N、P、Q为所在边的中点,
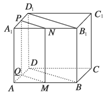
则过这四个点中的任意两点的直线都与面DBB1D1平行,这种情形共有6条;同理,经过BC、CD、B1C1、C1D1四条棱的中点,也有6条;故共有12条,故选D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com