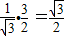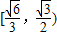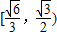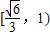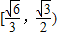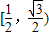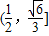已知正△ABC的顶点A在平面α上,顶点B、C在平面α的同一侧,D为BC的中点,若△ABC在平面α上的投影是以A为直角顶点的三角形,则直线AD与平面α所成角的正弦值的范围为 .
【答案】
分析:根据题意,作图,设正三角形的边长为1,设出B,C到面的距离分别为a,b,,则DG的长度为两者和的一半,通过解直角三角形用a,b表示出DG,得出sinα的表达式后,再根据条件,利用函数、不等式知识研究其最值.
解答: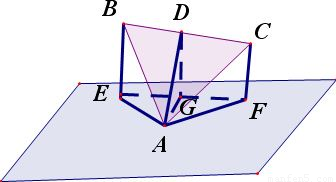
解:设正△ABC边长为1,则线段AD=
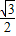
设B,C到平面α距离分别为a=BE,b=CF,
则D到平面α距离为hDG=
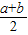
射影三角形两直角边的平方分别为1-a
2,1-b
2,
设线段BC射影长为c,则1-a
2+1-b
2=c
2,(1)
又线段AD射影长为
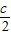
,
所以(
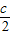
)
2+
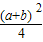
=AD
2=

,(2)
由(1)(2)联立解得 ab=

,
所以sinα=
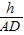
=
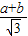
=
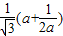
≥
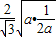
=
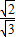
=
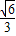
,当a=b=
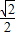
时等号成立.
此时BC与α平行.
令函数f(a)=
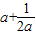
,0<a<1,根据B,C关于D的对称性,不妨研究
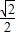
≤a<1的情形.
由于函数f′(a)=1-
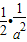
=
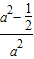
当
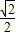
≤a<1时,f′(a)>0,
所以f(a)在(
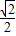
1)上单调递增,当a趋近于1时,f(a)趋近于1+

=

.,
sinα趋近于
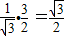
所以sinα的取值范围为
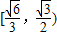
故答案为:
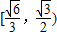 点评:
点评:本题考查线面角的大小度量,考查空间想象、计算、推理论证能力.以及建立数学模型,解决数学模型的能力.

 解:设正△ABC边长为1,则线段AD=
解:设正△ABC边长为1,则线段AD=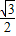
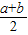
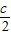 ,
,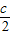 )2+
)2+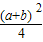 =AD2=
=AD2= ,(2)
,(2) ,
,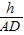 =
=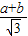 =
=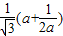 ≥
≥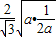 =
=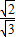 =
=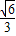 ,当a=b=
,当a=b=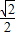 时等号成立.
时等号成立.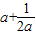 ,0<a<1,根据B,C关于D的对称性,不妨研究
,0<a<1,根据B,C关于D的对称性,不妨研究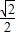 ≤a<1的情形.
≤a<1的情形.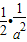 =
=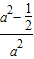
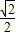 ≤a<1时,f′(a)>0,
≤a<1时,f′(a)>0,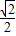 1)上单调递增,当a趋近于1时,f(a)趋近于1+
1)上单调递增,当a趋近于1时,f(a)趋近于1+ =
= .,
.,