
(5分)(2011•天津)已知双曲线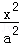 ﹣
﹣ =1(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),则双曲线的焦距为( )
A.2 | B.2 | C.4 | D.4 |
B
解析试题分析:根据题意,点(﹣2,﹣1)在抛物线的准线上,结合抛物线的性质,可得p=4,进而可得抛物线的焦点坐标,依据题意,可得双曲线的左顶点的坐标,即可得a的值,由点(﹣2,﹣1)在双曲线的渐近线上,可得渐近线方程,进而可得b的值,由双曲线的性质,可得c的值,进而可得答案.
解:根据题意,双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),
即点(﹣2,﹣1)在抛物线的准线上,又由抛物线y2=2px的准线方程为x=﹣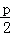 ,则p=4,
,则p=4,
则抛物线的焦点为(2,0);
则双曲线的左顶点为(﹣2,0),即a=2;
点(﹣2,﹣1)在双曲线的渐近线上,则其渐近线方程为y=± x,
x,
由双曲线的性质,可得b=1;
则c= ,则焦距为2c=2
,则焦距为2c=2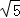 ;
;
故选B.
点评:本题考查双曲线与抛物线的性质,注意题目“双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1)”这一条件的运用,另外注意题目中要求的焦距即2c,容易只计算到c,就得到结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
[2014·张家口模拟]设F1,F2是双曲线x2- =1的两个焦点,P是双曲线上的一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于 ( )
=1的两个焦点,P是双曲线上的一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于 ( )
A.4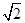 | B.8 | C.24 | D.48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com