练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设的所有排列的集合为；，记

    ，；求．（其中表示集合的元素个数）．


    解析:

    ：我们一般地证明，若，对于前个正整数的所有排列构成的集合，若，，则．

    下面用数学归纳法证明：．

    当时，由排序不等式知，集合中的最小元素是，最大元素是

    ．又，，

    ，

    ，所以，=共有11=个元素．因此，时命题成立．假设命题在（）时成立；考虑命题在时的情况．对于的任一排列，恒取，得到的一个排列，

    则．由归纳假设知，此时取遍区间

    上所有整数．

    再令，则，

    再由归纳假设知，取遍区间

    上的所有整数．

    因为，所以，取遍区间

    上的所有整数．即命题对也成立．由数学归纳法知，命题成立．

    由于  ，从而，集合

    的元素个数为．特别是，当时，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知二次函数f（t）=at2-
    		b
    t+
    1
    4a
    （t∈R）有最大值，且最大值为正实数，集合A={x|
    x-a
    x
    ＜0}，集合B={x|x2＜b2}
    （1）求集合A和B；
    （2）定义：“A-B={x∈A，且x∉B}”设a，b，x均为整数，且x∈A．记P（E）为x取自集合A-B的概率，P（F）x取集合A∩B的概率．已知P（E）=
    2
    3
    ，P（F）=
    1
    3
    ．记满足上述条件的所有a的值从小到大排列构成的数列为{an}，所有b的值从小到大排列构成数列{bn}．
    ①求a1，a2，a3和b1，b2，b3；
    ②请写出数列{an}和{bn}的通项公式（不必证明）；
    ③如果在函数中f（t）中，a=an，b=bn，记f（t）的最大值为g（n），cn=
    1-12g(n)
    4g(n)
    ，Sn=c1c2+c2c3+…+cncn+1，求证：Sn＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设{an}是集合{2s+2t|0≤s＜t，且s，t∈Z}中所有的数从小到大排列成的数列，即a1=3，a2=5，a3=6，a4=9，a5=10，a6=12…，将数列{an}中各项按照上小下大，左小右大的原则排成如下等腰直角三角形数表：
    3
    5   6
    9   10   12
    …
    则第四行四个数分别为
     
    ；且a2012=
     
    （用2s+2t形式表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （Ⅰ）设｛an｝是集合中所有的数从小到大排列成的数列，即a1＝3，a2＝5，a3＝6，a4＝9，a5＝10，a6＝12，……

    将数列｛an｝各项按照上小下大，左小右大的原则写成如下的三角形数表：

    （i）写出这个三角形数表的第四行、第五行各数;

    （ii）求a100．

    （Ⅱ）（本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分）

    设｛bn｝是集合中所有的数从小到大排列成的数列，已知bk =1160，求k．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    22.（Ⅰ）设｛an｝是集合｛2t+2s|0≤s＜t，且s，tZ｝中所有的数从小到大排列成的数列，即a1=3，a2=5，a3=6，a4=9，a5=10，a6=12，…….

    将数列｛an｝各项按照上小下大，左小右大的原则写成如下的三角形数表：

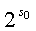
    （ⅰ）写出这个三角形数表的第四行、第五行各数；

    （ⅱ）求a100.

    （Ⅱ）（本小题为附加题）

    设｛bn｝是集合｛2t+2s+2r|0≤r<s<t，且r，s，tZ｝中所有的数从小到大排列成的数列.

    已知bk=1160，求k.

    查看答案和解析>>

    同步练习册答案