
已知 ,
, ,且
,且
(1)求函数
 的单调增区间;
的单调增区间;
(2)证明无论 为何值,直线
为何值,直线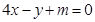 与函数
与函数 的图象不相切.
的图象不相切.
(1)单调增区间为 和
和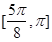 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)首先由向量的数量积及坐标运算得函数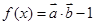 的解析式,利用正弦函数的单调区间即可求得该函数的单调区间;(2)注意直线
的解析式,利用正弦函数的单调区间即可求得该函数的单调区间;(2)注意直线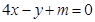 的斜率为4,那么要证明无论
的斜率为4,那么要证明无论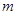 为何值,直线
为何值,直线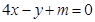 与函数
与函数 的图象不相切,就只需通过求导说明函数的导数值不可能等于4即可.
的图象不相切,就只需通过求导说明函数的导数值不可能等于4即可.
试题解析:(1)∵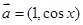 ,
,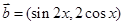 ,且
,且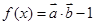
∴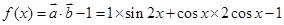 1分
1分
=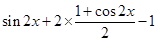 =
=
=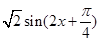 3分
3分
令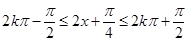 ,解之得
,解之得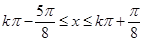 4分
4分
又∵ ∴
∴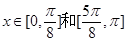
故函数
 的单调增区间为
的单调增区间为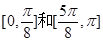 6分
6分
(2)∵
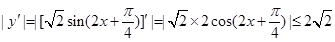 9分
9分
∴曲线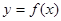 的切线斜率的取值范围为
的切线斜率的取值范围为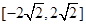
而直线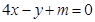 的斜率为
的斜率为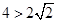 ,
11分
,
11分
∴证明无论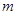 为何值,直线
为何值,直线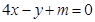 与函数
与函数 的图象不相切 12分
的图象不相切 12分
考点:1、向量的数量积及坐标运算;2、三角变换及三角函数的单调区间;3、导数的应用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源:2011-2012学年广东省高三第一次模拟考试文科数学 题型:解答题
.(本小题满分12分)
已知向量 ,且
,且
(1)求 的解析式和它的最小正周期;
的解析式和它的最小正周期;
(2)求函数 的值域。
的值域。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com