练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．$y=\frac{1}{x}$在点A（1，1）处的切线方程是（　　）
    A．x+y-2=0B．x-y+2=0C．x+y+2=0D．x-y-2=0

    分析 求出导数，得到切线的斜率，然后求解切线方程．

    解答 解：$y=\frac{1}{x}$，可得$y′=-\frac{1}{{x}^{2}}$，切线的斜率为：-1，
    $y=\frac{1}{x}$在点A（1，1）处的切线方程是：y-1=-（x-1），
    即x+y-2=0．
    故选：A．

    点评 本题考查函数的导数的应用，切线方程的求法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．设Sn是整数组成的数列{an}的前n项和，且$\frac{4{S}_{n}}{{a}_{n}}$=an+2（n∈N*），又数列{bn}是a1为首项，公比为a2-a1的等比数列．
    （1）求数列{an}、{bn}的通项公式；
    （2）记cn=an+$\frac{24}{{b}_{n}}$，求数列{cn}的最小项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．如图，长方体ABCD-A1B1C1D1中，与直线D1C异面的棱所在的直线有（　　）条．
    A．2B．4C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设全集为R，函数$f（x）=\sqrt{2-x}$的定义域为M，则∁RM为（　　）
    A．（2，+∞）B．（-∞，2）C．（-∞，2]D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．求值：
    ①cos36°cos72°+tan15°tan30°+tan15°+tan30°
    ②$ln（{e\sqrt{e}}）+{log_2}（{{{log}_2}16}）-{（{\sqrt{2\sqrt{2}}}）^{\frac{4}{3}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数f（x）=2x+3，则f（-1）=（　　）
    A．2B．1C．$\frac{5}{2}$D．$\frac{7}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．下列判断中不正确的是（　　）
    A．r为变量间的相关系数，|r|值越大，线性相关程度越高
    B．在平面直角坐标系中，可以用散点图发现变量之间的变化规律
    C．线性回归方程代表了观测值x、y之间的关系
    D．任何一组观测值都能得到具有代表意义的回归直线方程

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

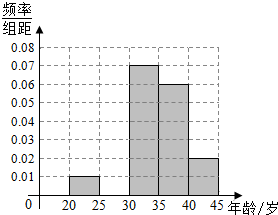    13．由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》，某部门从参加创作的507名画师中随机抽出100名画师，得到画师年龄的频率分布表如下表所示．
    （Ⅰ）求a，b的值；并补全频率分布直方图；
    （Ⅱ）根据频率分布直方图估计这507名画师年龄的平均数；
    （Ⅲ）在抽出的[20，25）岁的5名画师中有3名男画师，2名女画师．在这5名画师中任选两人去参加某绘画比赛，选出的恰好是一男一女的概率是多少？
    分组（岁）频数频率
    [20，25）50.050
    [25，30）a0.200
    [30，35）35b
    [35，40）300.300
    [40，45）100.100
    合计1001.00

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设椭圆方程为x2+$\frac{y^2}{4}$=1，过点M（0，1）的直线L交椭圆于点A、B，O为坐标原点，点P满足$\overrightarrow{OP}=\frac{1}{2}（\overrightarrow{OA}+\overrightarrow{OB}）$，当L绕点M旋转时，求
    （1）当L的斜率为1时，求三角形ABC的面积；
    （2）动点P的轨迹方程．

    查看答案和解析>>

    同步练习册答案