练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

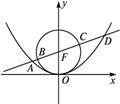
    如图,过抛物线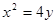焦点的直线依次交抛物线与圆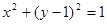于点A、B、C、D,则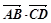的值是________

     

    【答案】

    1

    【解析】解：设A、D的坐标分别为（x1，y1），（x2，y2），依题意知焦点F（0，1），则设直线AD方程为：y=kx+1，

    联立

     y=kx+1

       消去x，得y2-（2+4k2）y+1=0，

    ∴y1+y2=2+4k2，y1•y2=1

    又根据抛物线定义得AF=y1+p/ 2 ，FD=y2+p/ 2 ，∴AF=y1+1，FD=y2+1

     AB • CD = |AB |• |CD |=(AF-BF)(FD-CF)=（AF-1）（FD-1）

    =y1•y2=1．

    故答案为1

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网已知抛物线G的顶点在原点，焦点在y轴正半轴上，点P（m，4）到其准线的距离等于5．
    （I）求抛物线G的方程；
    （II）如图，过抛物线G的焦点的直线依次与抛物线G及圆x2+（y-1）2=1交于A、C、D、B四点，试证明|AC|•|BD|为定值；
    （III）过A、B分别作抛物G的切线l1，l2且l1，l2交于点M，试求△ACM与△BDM面积之和的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年浙江省绍兴市高三教学质量调测理科数学试卷（解析版） 题型：解答题

    （本小题满分15分）如图，过抛物线焦点F的直线l与抛物线交于A，B两点（A在第一象限），点C（0，t）（t>1）.

    （I）若△CBF，△CFA，△CBA的面积成等差数列，求直线l的方程；

    （II）若，且∠FAC为锐角，试求t的取值范围。

     

    查看答案和解析>>

    科目：高中数学 来源：2010年江苏省南通市如东县栟茶高级中学高考数学一模试卷（解析版） 题型：解答题

    已知抛物线G的顶点在原点，焦点在y轴正半轴上，点P（m，4）到其准线的距离等于5．
    （I）求抛物线G的方程；
    （II）如图，过抛物线G的焦点的直线依次与抛物线G及圆x2+（y-1）2=1交于A、C、D、B四点，试证明|AC|•|BD|为定值；
    （III）过A、B分别作抛物G的切线l1，l2且l1，l2交于点M，试求△ACM与△BDM面积之和的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2010年高考数学最有可能考的50题（解析版） 题型：解答题

    已知抛物线G的顶点在原点，焦点在y轴正半轴上，点P（m，4）到其准线的距离等于5．
    （I）求抛物线G的方程；
    （II）如图，过抛物线G的焦点的直线依次与抛物线G及圆x2+（y-1）2=1交于A、C、D、B四点，试证明|AC|•|BD|为定值；
    （III）过A、B分别作抛物G的切线l1，l2且l1，l2交于点M，试求△ACM与△BDM面积之和的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2010年福建省厦门市高三3月质量检查数学试卷（理科）（解析版） 题型：解答题

    已知抛物线G的顶点在原点，焦点在y轴正半轴上，点P（m，4）到其准线的距离等于5．
    （I）求抛物线G的方程；
    （II）如图，过抛物线G的焦点的直线依次与抛物线G及圆x2+（y-1）2=1交于A、C、D、B四点，试证明|AC|•|BD|为定值；
    （III）过A、B分别作抛物G的切线l1，l2且l1，l2交于点M，试求△ACM与△BDM面积之和的最小值．

    查看答案和解析>>

    同步练习册答案