
| A. | a≥2+$\sqrt{3}$ | B. | 0<a<2-$\sqrt{3}$ | C. | a≥2+$\sqrt{3}$或0<a<1 | D. | a≥2+$\sqrt{3}$或0<a<2-$\sqrt{3}$ |
分析 由g(x)=x2-(a+$\frac{1}{a}})x+1}$)x+1开口向上,对称轴大于1,且g(1)<0,可得y=|x2-(a+$\frac{1}{a}})x+1}$)x+1|在[1,2]上是增函数,结合复合函数的单调性得到关于a的不等式组求解.
解答 解:∵a>0,∴a+$\frac{1}{a}})x+1}$≥2,则函数y=x2-(a+$\frac{1}{a}})x+1}$)x+1的对称轴为x=$\frac{a+\frac{1}{a}}{2}≥1$,
令g(x)=x2-(a+$\frac{1}{a}})x+1}$)x+1,∵g(1)=2-(a+$\frac{1}{a}$)<0,
∴y=|x2-(a+$\frac{1}{a}})x+1}$)x+1|在[1,2]上是增函数,
∴要使函数f(x)=loga|x2-(a+$\frac{1}{a}})x+1}$)x+1|在[1,2]上是增函数,
则$\left\{\begin{array}{l}{a>1}\\{\frac{a+\frac{1}{a}}{2}≥2}\end{array}\right.$,解得a$≥2+\sqrt{3}$.
故选:A.
点评 本题考查对数函数的图象和性质,考查复合函数的单调性,考查数学转化思想方法,是中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
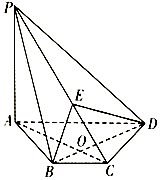 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.
把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
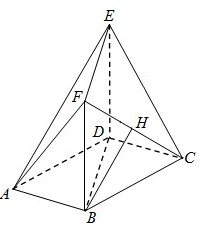 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com