
【题目】定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(sinα)<f(cosβ)
C.f(cosα)<f(cosβ)
D.f(sinα)>f(cosβ)
【答案】D
【解析】解:由题意:可知f(x+2)=f(x), ∴f(x)是周期为2的函数,
∵f(x)在[﹣3,﹣2]上为减函数,
∴f(x)在[﹣1,0]上为减函数,
又∵f(x)为偶函数,根据偶函数对称区间的单调性相反,
∴f(x)在[0,1]上为单调增函数.
∵在锐角三角形中,π﹣α﹣β< ![]()
∴π﹣α﹣β ![]() ,即
,即 ![]() ,
,
∴ ![]() >α>
>α> ![]() ﹣β>0,
﹣β>0,
∴sinα>sin( ![]() )=cosβ;
)=cosβ;
∵f(x)在[0,1]上为单调增函数.
所以f(sinα)>f(cosβ),
故选:D.
根据f(x+2)=f(x),所以函数的周期为2,在[﹣3,﹣2]上是减函数,可得f(x)在[﹣1,0]上为减函数,因为f(x)为偶函数,所以f(x)在[0,1]上为单调增函数.在根据α,β是锐角三角形的两个内角,利用三角函数诱导公式化简可得答案.


科目:高中数学 来源: 题型:
【题目】先后掷子(子的六个面上分别标有1,2,3,4,5,6个点)两次,落在水平桌面后,记正面朝上的点数分别为x,y,设事件A为“x+y为偶数”,事件B为“x,y中有偶数且x≠y”,则概率P(B|A)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足a1=2,Sn-4Sn-1-2=0(n≥2,n∈Z).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=log2an,Tn为{bn}的前n项和,求证![]() <2.
<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.
(1)求A中学至少有1名学生入选代表队的概率;
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示,将f(x)的图象向左平移
)的部分图象如图所示,将f(x)的图象向左平移 ![]() 个单位后的解析式为( )
个单位后的解析式为( ) 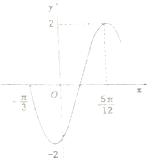
A.y=2sin(2x﹣ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin(2x)
D.y=2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB.现将四边形ABCD沿EF折起,使平面ABEF⊥平面EFDC.
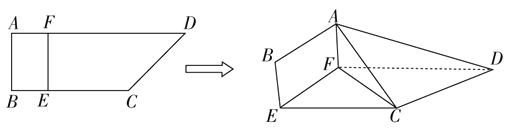
(Ⅰ)若BE=1,是否在折叠后的线段AD上存在一点P,且![]() ,使CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
,使CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
(Ⅱ)求三棱锥A-CDF的体积的最大值,并求出此时二面角E-AC-F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z在复平面内对应的点在第四象限,且z是方程x2﹣4x+5=0的根.
(1)求复数z;
(2)复数w=a﹣ ![]() (a∈R)满足|w﹣z|<2
(a∈R)满足|w﹣z|<2 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=(2m2+3m﹣2)+(m2+m﹣2)i,(m∈R)根据下列条件,求m值.
(1)z是实数;
(2)z是虚数;
(3)z是纯虚数;
(4)z=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com