
已知a,b是不相等的正数,在a,b之间分别插入m个正数a1,a2, ,am和正数b1,b2, ,
bm,使a,a1,a2, ,am,b是等差数列,a,b1,b2, ,bm,b是等比数列.
(1)若m=5,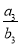 =
=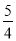 ,求
,求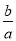 的值;
的值;
(2)若b=λa(λ∈N*,λ≥2),如果存在n (n∈N*,6≤n≤m)使得an-5=bn,求λ的最小值及此时m的值;
(3)求证:an>bn(n∈N*,n≤m).
(1) ;(2)
;(2) 最小值为4,此时
最小值为4,此时 为29;(3)详见解析
为29;(3)详见解析
【解析】
试题分析:(1)根据题意m=5时,共有7项,设等差数列的公差为 ,等比数列的公比为
,等比数列的公比为 ,则
,则 ,表示出
,表示出 ,又由
,又由 ,可得到
,可得到 ,解得
,解得 ;(2)由条件得
;(2)由条件得 ,即
,即 ,从而得
,从而得 ,又由于
,又由于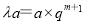 ,即
,即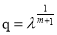 ,从而得
,从而得 ,又题中有
,又题中有 ,可得
,可得 , 化简消去a得:
, 化简消去a得: ,观察此式结构特征:
,观察此式结构特征: ,则要求
,则要求 为有理数.即
为有理数.即 必须为有理数,而
必须为有理数,而 ,可将
,可将 用数字代入检验: 若
用数字代入检验: 若 ,则
,则 为无理数,不满足条件; 同理,
为无理数,不满足条件; 同理, 不满足条件; 当
不满足条件; 当 时,
时,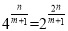 .要使
.要使 为有理数,则
为有理数,则 必须为整数,要满足
必须为整数,要满足  ,可解得
,可解得 ;(3)可假设
;(3)可假设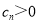 ,
, 为数列
为数列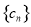 的前
的前 项的和,我们易先证:若
项的和,我们易先证:若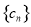 为递增数列,则
为递增数列,则 为递增数列;同理可证,若
为递增数列;同理可证,若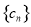 为递减数列,则
为递减数列,则 为递减数列;由于a和b的大小关系不确定,故要对其分类讨论:①当
为递减数列;由于a和b的大小关系不确定,故要对其分类讨论:①当 时,
时,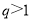 .当
.当 时,
时, .即
.即 ,即
,即 .因为
.因为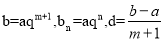 ,所以
,所以 ,即
,即 ,即
,即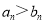 ;②当
;②当 时,同理可求得
时,同理可求得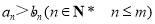 .
.
试题解析:(1)设等差数列的公差为 ,等比数列的公比为
,等比数列的公比为 ,
,
则 .
.
 . 2分
. 2分
因为 ,所以
,所以 ,解得
,解得 . 4分
. 4分
(2)因为 ,所以
,所以 ,从而得
,从而得 .
.
因为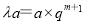 ,所以
,所以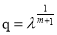 ,从而得
,从而得 .
.
因为 ,所以
,所以 .
.
因为 ,所以
,所以 (*). 6分
(*). 6分
因为 ,所以
,所以 为有理数.
为有理数.
要使(*)成立,则 必须为有理数.
必须为有理数.
因为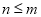 ,所以
,所以 .
.
若 ,则
,则 为无理数,不满足条件.
为无理数,不满足条件.
同理, 不满足条件. 8分
不满足条件. 8分
当 时,
时,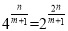 .要使
.要使 为有理数,则
为有理数,则 必须为整数.
必须为整数.
又因为 ,所以仅有
,所以仅有 满足条件.
满足条件.
所以 ,从而解得
,从而解得 .
.
综上, 最小值为4,此时
最小值为4,此时 为29. 10分
为29. 10分
(3)设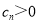 ,
, 为数列
为数列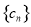 的前
的前 项的和.
项的和.
先证:若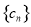 为递增数列,则
为递增数列,则 为递增数列.
为递增数列.
证明:当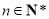 时,
时, .
.
因为 ,所以
,所以 ,即数列
,即数列 为递增数列.
为递增数列.
同理可证,若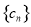 为递减数列,则
为递减数列,则 为递减数列. 12分
为递减数列. 12分
①当 时,
时,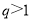 .当
.当 时,
时, .
.
即 ,即
,即 .
.
因为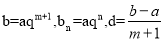 ,
,
所以 ,即
,即 ,即
,即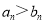 .
.
②当 时,
时, ,当
,当 时,
时,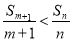 .
.
即 .
.
因为 ,所以
,所以 .以下同①.
.以下同①.
综上,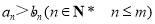 . 16分
. 16分
考点:1.等差,等比数列的基本运算;2.函数的最值;3.代数式的处理


科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,设曲线C1: 所围成的封闭图形的面积为
所围成的封闭图形的面积为
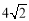 ,曲线C1上的点到原点O的最短距离为
,曲线C1上的点到原点O的最短距离为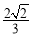 .以曲线C1与坐标轴的交点为顶点的椭圆记
.以曲线C1与坐标轴的交点为顶点的椭圆记
为C2.
(1)求椭圆C2的标准方程;
(2)设AB是过椭圆C2中心O的任意弦,l是线段AB的垂直平分线.M是l上的点(与O不重合).
①若MO=2OA,当点A在椭圆C2上运动时,求点M的轨迹方程;
②若M是l与椭圆C2的交点,求△AMB的面积的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:填空题
袋中有2个红球,2个蓝球,1个白球,从中一次取出2个球,则取出的球颜色相同的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
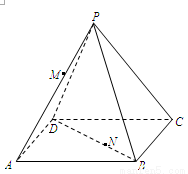
如图,在正四棱锥P-ABCD中,PA=AB= ,点M,N分别在线段PA和BD上,BN=
,点M,N分别在线段PA和BD上,BN= BD.
BD.
(1)若PM= PA,求证:MN⊥AD;
PA,求证:MN⊥AD;
(2)若二面角M-BD-A的大小为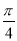 ,求线段MN的长度.
,求线段MN的长度.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,且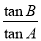 +1=
+1= .
.
(1)求B;
(2)若cos(C+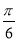 )=
)=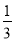 ,求sinA的值.
,求sinA的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
已知m,n是不重合的两条直线,α,β是不重合的两个平面.下列命题:
①若α⊥β,m⊥α,则m∥β; ②若m⊥α,m⊥β,则α∥β;
③若m∥α,m⊥n,则n⊥α; ④若m∥α,m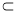 β,则α∥β.
β,则α∥β.
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟理科数学试卷(解析版) 题型:填空题
已知集合A={4},B={1,2},C={1,3,5},从这三个集合中各取一个元素构成空间直角坐标系中的点的坐标,则确定的不同点的个数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com