
已知:向量 ,O为坐标原点,动点M满足:
,O为坐标原点,动点M满足: .
.
(1) 求动点 M 的轨迹 C 的方程;
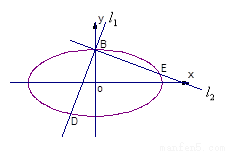
(2)已知直线 、
、 都过点
都过点 ,且
,且 ,
, 、
、 与轨迹C分别交于点D、E.是否存在这样的直线
与轨迹C分别交于点D、E.是否存在这样的直线 、
、 ,使得△BDE是等腰直角三角形?若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
,使得△BDE是等腰直角三角形?若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
设点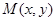 ,则
,则 …… 1分
…… 1分
∵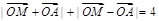
∴ ……… ……… ……… 2分
……… ……… ……… 2分
∴点 M 的轨迹C是以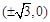 为焦点,长轴长为 4 的椭圆……… ……
……… 4分
为焦点,长轴长为 4 的椭圆……… ……
……… 4分
∴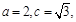 ∴
∴ 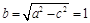
∴ 动点M 的轨迹 C的方程为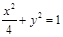 ……… ………
……… 6分
……… ………
……… 6分
(2)由(1)知,轨迹C是椭圆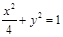 ,点
,点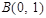 是它的上顶点,
是它的上顶点,
设满足条件的直线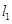 、
、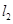 存在,直线
存在,直线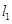 的方程为
的方程为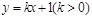 ①
①
则直线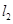 的方程为
的方程为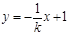 ,② ……… ………
……… 7分
,② ……… ………
……… 7分
将①代入椭圆方程并整理得: ,可得
,可得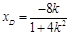 ,则
,则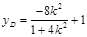 .
.
将②代入椭圆方程并整理得: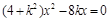 ,可得
,可得 ,则
,则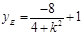 .
.
由△BDE是等腰直角三角形得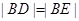

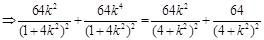
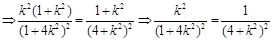

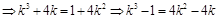
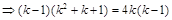 …………11分
…………11分
∴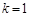 或
或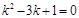 ④…………………………………………12分
④…………………………………………12分
∵方程④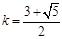 或
或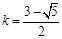 .
.
∴即满足条件的直线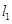 、
、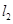 存在,共有3组.
存在,共有3组.
【解析】略


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:2012届安徽省芜湖一中高三上学期第二次月考理科数学试卷 题型:解答题
已知:向量 ,O为坐标原点,动点M满足:
,O为坐标原点,动点M满足: .
.
(1) 求动点 M的轨迹 C的方程;
(2)已知直线 、
、 都过点
都过点 ,且
,且 ,
, 、
、 与轨迹C分别交于点D、E.是否存在这样的直线
与轨迹C分别交于点D、E.是否存在这样的直线 、
、 ,使得△BDE是等腰直角三角形?若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
,使得△BDE是等腰直角三角形?若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省名校名师新编“百校联盟”高三第一次调研考试数学理卷 题型:解答题
已知:向量 (O为坐标原点).
(O为坐标原点).
(Ⅰ)求 的最大值及此时
的最大值及此时 的值组成的集合;
的值组成的集合;
(Ⅱ)若A点在直线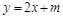 上运动,求实数
上运动,求实数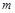 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知:向量![]() ,O为坐标原点,动点M满足:
,O为坐标原点,动点M满足:![]() .
.
求动点 M 的轨迹 C 的方程;
(2)已知直线![]() 、
、![]() 都过点
都过点![]() ,且
,且![]() ,
,![]() 、
、![]() 与轨迹C分别交于点D、E,试探究是否存在这样的直线?使得△BDE是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
与轨迹C分别交于点D、E,试探究是否存在这样的直线?使得△BDE是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com