
分析 (1)利用倍角公式可得:f(x)=10$sin(x+\frac{π}{6})$+5,即可得出函数f(x)的最小正周朋T;
(2)(i)利用三角函数的平移变换法则可得:g(x)=10sinx+5-a,当sinx=1时,函数g(x)取得最大值10+5-a=2,解得a.
(ii)由g(x)=10sinx-8>0,解得sinx>$\frac{4}{5}$.解得2kπ+arcsin$\frac{4}{5}$<x<2kπ+π-arcsin$\frac{4}{5}$,由于$\frac{π}{4}<$arcsin$\frac{4}{5}$$<\frac{π}{3}$,可得$\frac{π}{2}$<2arcsin$\frac{4}{5}$<$\frac{2π}{3}$,可知对于一个确定的整式k,都有2kπ+π-arcsin$\frac{4}{5}$-(2kπ+arcsin$\frac{4}{5}$)=π-2arcsin$\frac{4}{5}$∈$(\frac{π}{3},\frac{π}{2})$.$\frac{π}{3}$>1,即可证明.
解答 (1)解:f(x)=5$\sqrt{3}$sinx+5(1+cosx)
=10$sin(x+\frac{π}{6})$+5,
∴函数f(x)的最小正周期T=2π;
(2)(i)解:将函数f(x)的图象向右平移$\frac{π}{6}$个单位长度,再向下平移a(a>0)个单位长度后得到函数g(x)的图象,
则g(x)=10sin$(x+\frac{π}{6}-\frac{π}{6})$+5-a=10sinx+5-a,
当sinx=1时,函数g(x)取得最大值10+5-a=2,解得a=13.
∴g(x)=10sinx-8.
(ii)证明:由g(x)=10sinx-8>0,解得sinx>$\frac{4}{5}$.
解得2kπ+arcsin$\frac{4}{5}$<x<2kπ+π-arcsin$\frac{4}{5}$,
∵$\frac{π}{4}<$arcsin$\frac{4}{5}$$<\frac{π}{3}$,∴$\frac{π}{2}$<2arcsin$\frac{4}{5}$<$\frac{2π}{3}$,
∴对于一个确定的整式k,都有2kπ+π-arcsin$\frac{4}{5}$-(2kπ+arcsin$\frac{4}{5}$)=π-2arcsin$\frac{4}{5}$∈$(\frac{π}{3},\frac{π}{2})$.
∵$\frac{π}{3}$>1,
∴存在无穷多个互不相同的正整数x0∈(2kπ+arcsin$\frac{4}{5}$,2kπ+π-arcsin$\frac{4}{5}$),
使得g(x0)>0.
点评 本题考查了三角函数的图象与性质、平移变换,考查了数形结合能力、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
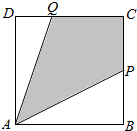 如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (6,7) | B. | (2,-1) | C. | (-2,1) | D. | (7,6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com