
 如图四边形ABCD为梯形,AD∥BC,∠ABC=90°,AD=2,AB=4,BC=5,图中阴影部分(梯形剪去一个扇形)绕AB旋转一周形成一个旋转体.
如图四边形ABCD为梯形,AD∥BC,∠ABC=90°,AD=2,AB=4,BC=5,图中阴影部分(梯形剪去一个扇形)绕AB旋转一周形成一个旋转体.分析 (1)旋转体为圆台挖去一个半球后的几何体,圆台的上下底面半径为AD,BC,高为AB,半球的半径为AD.于是几何体的表面积为圆台侧面积与底面积半球面积的和;
(2)体积为圆台体积与半球体积的差.
解答 解:(1)旋转后的几何体是一个圆台从上面挖去一个半球,圆台的上下底面半径分别为2,5高为4,半球半径为2.
圆台的母线长为CD=$\sqrt{(5-2)^{2}+{4}^{2}}$=5.
∴${S_{半球}}=\frac{1}{2}×4π×{2^2}=8π$,S圆台侧=π×(2+5)×5=35π,${S_{圆台底}}=π×{5^2}=25π$,
∴旋转体的表面积为S表=8π+35π+25π=68π.
(2)V圆台=$\frac{1}{3}$(4π+25π+10π)•4=52π,${V_{半球}}=\frac{4π}{3}×{2^3}×\frac{1}{2}=\frac{16π}{3}$,
∴旋转体的体积为$V=52π-\frac{16π}{3}=\frac{140π}{3}$.
点评 本题考查了旋转体的结构特征,面积与体积计算,属于中档题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
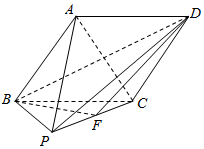 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
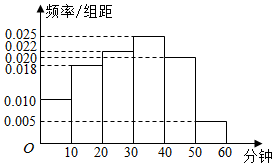 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 9个 | C. | 12个 | D. | 24个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com