


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
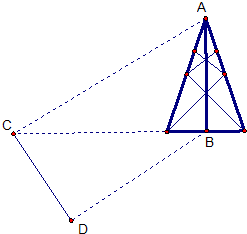 (2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB.
(2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB.查看答案和解析>>
科目:高中数学 来源: 题型:
(2008•海珠区一模)用二分法求方程x3-x-1=0在区间(0,2]内的实数解(精确到0.1),其参考数据如下:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com