练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    非零向量数学公式、数学公式，“数学公式+数学公式=0”是“数学公式∥数学公式”的________条件．

    充分不必要
    分析：我们可以根据充要条件的定义进行判断，由于，可得到，进而推出；而且推不出，故为充分不必要条件．
    解答：由于，则，所以；
    又由，则，不一定有．
    故?为真命题且?为假命题，
    故答案为：充分不必要．
    点评：本题考查的判断充要条件的方法，我们可以根据充要条件的定义进行判断，若p?q为真命题且q?p为假命题，则命题p是命题q的充分不必要条件．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知非零向量与满足()·=0且·=，则△ABC为(    )

    A.三边均不相等的三角形         B.直角三角形

    C.等腰非等边三角形             D.等边三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若a为非零向量,a·b=0,则满足此条件的向量b有(    )

    A.1个             B.2个             C.有限个           D.无限个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题是真命的是(    )

    A.分别表示空间向量的有向线段所在的直线是异面直线，则这两个向量不是共面向量

    B.若|a|=|b|,则a、b的长度相等而方向相同或相反

    C.若向量、满足||＞||,且与同向，则＞

    D.若两个非零向量与满足+=0，则∥

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知非零向量与满足()·=0，且()=．则△ABC为(    )

    A．三边均不相等的三角形           B．直角三角形

    C．等腰非等边三角形               D．等边三角形

    查看答案和解析>>

    科目：高中数学 来源：2012届福建省泉州市高三上学期期中理科数学试卷 题型：选择题

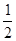    已知非零向量与满足(+)·=0且·= , 则△ABC为(     )

    A.  等边三角形       B.  直角三角形     C. 等腰三角形     D. 等腰直角三角形

     

    查看答案和解析>>

    同步练习册答案