
已知aÎR,函数f(x)=x3−3x2+3ax−3a+3
(Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当xÎ[0,2]时,求|f(x)|的最大值.
【命题意图】本题考查导数的几何意义,导数应用等基础知识,同时考查推理论证能力,分类讨论等分析问题和解决问题的能力
【答案解析】
(Ⅰ)由题意f ¢(x)=3x2−6x+3a,故f ¢(1)=3a−3.又f(1)=1,所以所求的切线方程为
y=(3a−3)x−3a+4
(Ⅱ)由于f ¢(x)=3(x−1)2+3(a−1),0x£2.故
(ⅰ)当a£0时,有f ¢(x) £0,此时f(x)在[0,2]上单调递减,故
|f(x)|max=max{|f(0)|,|f(2)|}=3−3a
(ⅱ)当a³1时,有f ¢(x) ³0,此时f(x)在[0,2]上单调递增,故
|f(x)|max=max{|f(0)|,|f(2)|}= 3a−1
(ⅲ)当0<a<1时,设x1=1−![]() ,x2=1+
,x2=1+![]() ,则
,则
0< x1< x2<2,f ¢(x)=3(x− x1)(x− x2)
列表如下:
| x | 0 | (0,x1) | x1 | (x1,x2) | x2 | (x2,2) | 2 |
| f ¢(x) | + | 0 | − | 0 | + | ||
| f (x) | 3−3a | 单调递增 | 极大值f (x1) | 单调递减 | 极小值f (x2) | 单调递增 | 3a−1 |
由于
f(x1)=1+2(1−a)![]() ,f(x2)=1−2(1−a)
,f(x2)=1−2(1−a)![]() ,
,
故
f(x1)+f(x2)=2>0,f(x1)×f(x2)=4(1−a)![]() >0
>0
从而
f(x1)>| f(x2)|.
所以
|f(x)|max=max{f(0),|f(2)|,f(x1)}
(1)当0<a<![]() 时,f(0)>|f(2)|.高考资源网
时,f(0)>|f(2)|.高考资源网
又
f(x1)− f(0)=2(1−a)![]() −(2−3a)=
−(2−3a)=![]() >0
>0
故
|f(x)|max= f(x1)=1+2(1−a)![]() .
.
(2)当![]() £a<1时,|f(2)|=f(2),且f(2)³f(0).
£a<1时,|f(2)|=f(2),且f(2)³f(0).
又
f(x1)− |f(2)|=2(1−a)![]() −( 3a −2)=
−( 3a −2)=![]()
所以
①当![]() £a<
£a<![]() 时,f(x1)> |f(2)|.故
时,f(x1)> |f(2)|.故
|f(x)|max= f(x1)=1+2(1−a)![]() .
.
②当![]() £a<1时,f(x1) £ |f(2)|.故
£a<1时,f(x1) £ |f(2)|.故
|f(x)|max=| f(2)|= 3a−1.
综上所述,
|f(x)|max=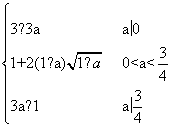


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源:2010年广东省高二下学期期末考试理科数学卷 题型:解答题
(14分)已知aÎR,函数f(x)=x| x-a |.
(1)当a=2时,求使f(x)=x成立的 的集合;
的集合;
(2)求函数y=f(x)在区间 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com