
已知数列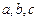 是各项均为正数的等差数列,公差为d(d
是各项均为正数的等差数列,公差为d(d 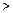 0).在
0).在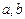 之间和b,c之间共插入
之间和b,c之间共插入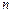 个实数,使得这
个实数,使得这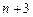 个数构成等比数列,其公比为q.
个数构成等比数列,其公比为q.
(1)求证: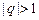 ;
;
(2)若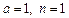 ,求
,求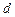 的值;
的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且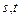 都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用
都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用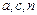 表示).
表示).
解:(1)由题意知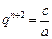 ,
, ,
,
又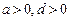 ,可得
,可得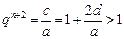 , ………………………………2分
, ………………………………2分
即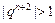 ,故
,故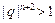 ,又
,又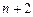 是正数,故
是正数,故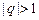 .………………………………4分
.………………………………4分
(2)由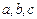 是首项为1、公差为
是首项为1、公差为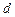 的等差数列,故
的等差数列,故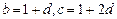 ,
,
若插入的这一个数位于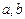 之间,则
之间,则 ,
,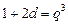 ,
,
消去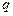 可
可 得
得 ,即
,即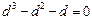 ,其正根为
,其正根为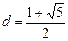 .………7分
.………7分
若插入的这一个数位于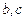 之间,则
之间,则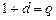 ,
,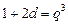 ,
,
消去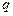 可得
可得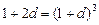 ,即
,即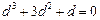 ,此方程无正根.
,此方程无正根.
故所求公差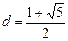 . ………………………………………9分
. ………………………………………9分
(3)由题意得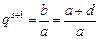 ,
, ,又
,又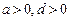 ,
,
故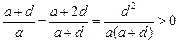 ,可
,可 得
得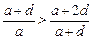 ,又
,又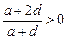 ,
,
故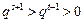 ,即
,即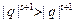 .
.
又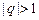 ,故有
,故有 ,即
,即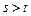 . ………………………………………12分
. ………………………………………12分
设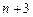 个数所构成的等比数列为
个数所构成的等比数列为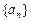 ,则
,则 ,
,
由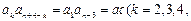 …,
…, ,可得
,可得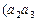 …
…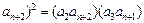 …
…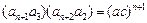 , ……………………14分
, ……………………14分
又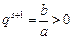 ,
,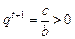 ,
,
由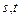 都为奇数,则q既可为正数,也可为负数,
都为奇数,则q既可为正数,也可为负数,
①若q为正数,则 …
…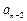
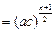 ,插入n个数的乘积为
,插入n个数的乘积为 ;
;
②若q为负数,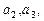 …
…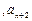 中共有
中共有 个负数,
个负数,
故 …
…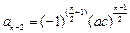 ,所插入的数的乘积为
,所插入的数的乘积为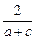
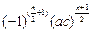 .
.
所以当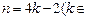 N*)时,所插入n个数的积为
N*)时,所插入n个数的积为 ;
;
当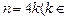 N*)时,所插入n个数的积为
N*)时,所插入n个数的积为 . …………………18分
. …………………18分
(另法:由又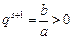 ,
,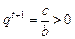 ,
,
由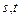 都为奇数,可知
都为奇数,可知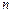 是偶数,q既可为正数也可为负数.
是偶数,q既可为正数也可为负数. …
…解析


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省高三高考模拟考试(八)文科数学试卷(解析版) 题型:解答题
已知数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意的
项和,对于任意的 ,满足关系式
,满足关系式
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的通项公式是
的通项公式是 ,前
,前 项和为
项和为 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有
查看答案和解析>>
科目:高中数学 来源:2014届云南省高二9月月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知数列 的各项均为正实数,且其前
的各项均为正实数,且其前 项和
项和 满足
满足 。(1)证明:数列
。(1)证明:数列 是等差数列;
是等差数列;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 。
。
查看答案和解析>>
科目:高中数学 来源:湖南省高考适应性测试数学(理) 题型:填空题
已知数列 是各项均为正整数的等差数列,公差
是各项均为正整数的等差数列,公差 ,且
,且 中任意两项之和也是该数列中的一项.
中任意两项之和也是该数列中的一项.
(1)若 ,则
,则 的取值集合为
;
的取值集合为
;
(2)若 ,则
,则 的所有可能取值的和为
.
的所有可能取值的和为
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com