
从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P( )等于( )
)等于( )
A. | B. | C. | D. |
科目:高中数学 来源: 题型:单选题
甲从学校乘车回家,途中有3个交通岗,假设在各交通岗遇红灯的事件是相互独立的,并且概率都是 ,则甲回家途中遇红灯次数的期望为( )
,则甲回家途中遇红灯次数的期望为( )
A. | B. | C.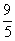 | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,那么互斥不对立的两个事件是
| A.恰有1名男生与恰有2名女生 |
| B.至少有1名男生与全是男生 |
| C.至少有1名男生与至少有1名女生 |
| D.至少有1名男生与全是女生 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
将高一(6)班52名学生分成A,B两组参加学校组织的义务植树活动,A组种植150棵大叶榕树苗,B组种植200棵红枫树苗.假定A,B两组同时开始种植.每名学生种植一棵大叶榕树苗用时 小时,种植一棵枫树苗用时
小时,种植一棵枫树苗用时 小时.完成这次植树任务需要最短时间为( )
小时.完成这次植树任务需要最短时间为( )
A. | B.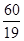 | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com