过抛物线y2=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )
A.y2=2x-1
B.y2=2x-2
C.y2=-2x+1
D.y2=-2x+2
【答案】
分析:设线段PQ所在的直线方程为 y-0=k(x-1),代入抛物线方程,利用一元二次方程、根与系数的关系求出线段PQ中点坐标
消去参数 k,即得线段PQ中点的轨迹方程.
解答:解:抛物线y
2=4x的焦点F(1,0),当线段PQ的斜率存在时,设线段PQ所在的直线方程为 y-0=k(x-1),
代入抛物线y
2=4x得,k
2x
2-(2k
2+4)x+k
2=0,∴x
1+x
2=
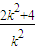
.
设线段PQ中点H( x,y ),则由中点公式得 x=

,∴y=k(x-1)=

,k=
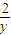
,
∴y
2=2x-2.当线段PQ的斜率存在时,线段PQ中点为焦点F(1,0),满足此式,
故线段PQ中点的轨迹方程是 y
2=2x-2,
故选B.
点评:本题考查求点的轨迹方程的方法,一元二次方程根与系数的关系,中点公式的应用,利用一元二次方程、根与系数的关系,中点公式求出线段PQ中点坐标是解题的关键.

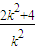 .
. ,∴y=k(x-1)=
,∴y=k(x-1)= ,k=
,k=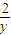 ,
,
