
设数列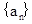 满足:
满足: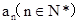 是整数,且
是整数,且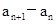 是关于x的方程
是关于x的方程
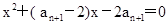 的根.
的根.
(1)若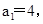 且n≥2时,
且n≥2时,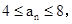 求数列{an}的前100项和S100;
求数列{an}的前100项和S100;
(2)若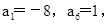 且
且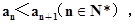 求数列
求数列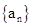 的通项公式.
的通项公式.
(1)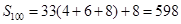 ; (2)
; (2)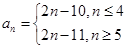 。
。
【解析】
试题分析:(1)由an+1-an是关于x的方程x2+( an+1-2)x-2an+1=0的根,
可得: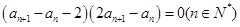 ,
,
所以对一切的正整数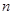 ,
,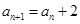 或
或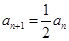 ,
,
若a1=4,且n≥2时,4≤an≤8,则数列{an}为: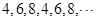
所以,数列{an}的前100项和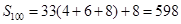 ;
;
(2)若a1=-8,根据an(n∈N*)是整数,an<an+1(n∈N*),且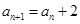 或
或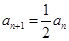
可知,数列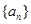 的前6项是:
的前6项是: 或
或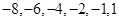 或
或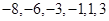 或
或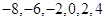 或
或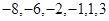
因为a6=1,所以数列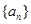 的前6项只能是
的前6项只能是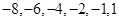 且
且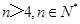 时,
时,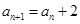 所以,数列{an}的通项公式是:
所以,数列{an}的通项公式是: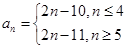
考点:本题主要考查数列的通项公式、求和公式,分段函数的概念。
点评:中档题,等比数列、等差数列相关内容,已是高考必考内容,其难度飘忽不定,有时突出考查求和问题,如“分组求和法”、“裂项相消法”、“错位相减法”等,有时则突出涉及数列的证明题。本题解法中,注意通过研究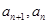 满足的条件,发现数列特征,确定得到数列的通项公式,带有普遍性。
满足的条件,发现数列特征,确定得到数列的通项公式,带有普遍性。


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源:2012届上海市崇明中学高三第一学期期中考试试题数学 题型:解答题
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
对于数列 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 称作周期为
称作周期为 的周期数列,
的周期数列, 的最小值称作数列
的最小值称作数列 的最小正周期,以下简称周期。例如当
的最小正周期,以下简称周期。例如当 时
时 是周期为
是周期为 的周期数列,当
的周期数列,当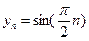 时
时 是周期为
是周期为 的周期数列。
的周期数列。
(1)设数列 满足
满足 (
( ),
), (
( 不同时为0),且数列
不同时为0),且数列 是周期为
是周期为 的周期数列,求常数
的周期数列,求常数 的值;
的值;
(2)设数列 的前
的前 项和为
项和为 ,且
,且 .
.
①若 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列 满足
满足 (
( ),
), ,
,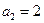 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,试问是否存在
,试问是否存在 ,使对任意的
,使对任意的 都有
都有 成立,若存在,求出
成立,若存在,求出 的取值范围;不存在, 说明理由;
的取值范围;不存在, 说明理由;
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省新课程高三上学期第三次适应性测试文科数学试卷(解析版) 题型:解答题
已知数列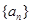 为等差数列,数列
为等差数列,数列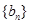 为等比数列且公比大于1,若
为等比数列且公比大于1,若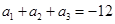 ,
,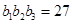 ,且
,且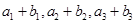 恰好是一各项均为正整数的等比数列的前三项.
恰好是一各项均为正整数的等比数列的前三项.
(1)求数列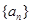 ,
,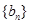 的通项公式;
的通项公式;
(2)设数列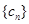 满足
满足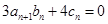
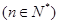 ,求
,求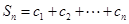 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省名校新高考研究联盟高三第二次联考文科数学试卷(解析版) 题型:解答题
.设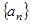 是公差不为零的等差数列,
是公差不为零的等差数列,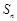 为其前
为其前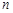 项和,满足:
项和,满足: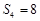 且
且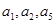 成等比数列.
成等比数列.
(I)求数列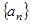 的通项公式;
的通项公式;
(II)设数列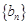 满足:
满足: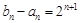 ,
,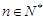 ,
,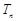 为数列
为数列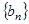 的前
的前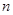 项和,问是否存在正整数
项和,问是否存在正整数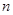 ,使得
,使得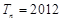 成立?若存在,求出
成立?若存在,求出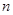 ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三下学期开学质量检测数学试卷 题型:解答题
(本题满分16分)
对于数列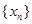 ,如果存在一个正整数
,如果存在一个正整数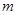 ,使得对任意的
,使得对任意的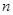 (
(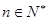 )都有
)都有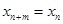 成立,那么就把这样一类数列
成立,那么就把这样一类数列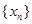 称作周期为
称作周期为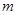 的周期数列,
的周期数列,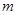 的最小值称作数列
的最小值称作数列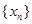 的最小正周期,以下简称周期.例如当
的最小正周期,以下简称周期.例如当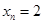 时
时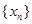 是周期为
是周期为 的周期数列,当
的周期数列,当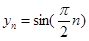 时
时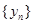 是周期为
是周期为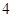 的周期数列.
的周期数列.
(1)设数列 满足
满足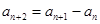 (
(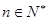 ),
),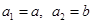 (
(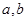 不同时为0),求证:数列
不同时为0),求证:数列 是周期为
是周期为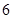 的周期数列,并求数列
的周期数列,并求数列 的前2012项的和
的前2012项的和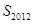 ;
;
(2)设数列 的前
的前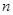 项和为
项和为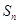 ,且
,且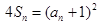 .
.
①若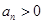 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若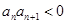 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列 满足
满足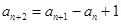 (
(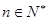 ),
),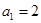 ,
,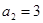 ,数列
,数列 的前
的前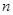 项和为
项和为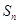 ,试问是否存在实数
,试问是否存在实数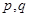 ,使对任意的
,使对任意的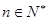 都有
都有 成立,若存在,求出
成立,若存在,求出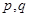 的取值范围;不存在,说明理由.
的取值范围;不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com