
【题目】已知函数![]() ,
,![]() ,
,![]() 图象与
图象与![]() 轴交于点
轴交于点![]() (
(![]() 异于原点),
异于原点),![]() 在
在![]() 处的切线为
处的切线为![]() ,
,![]() 图象与
图象与![]() 轴交于点
轴交于点![]() 且在该点处的切线为
且在该点处的切线为![]() ,并且
,并且![]() 与
与![]() 平行.
平行.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)已知实数![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(Ⅲ)令![]() ,给定
,给定![]() ,对于两个大于1的正数
,对于两个大于1的正数![]() ,存在实数
,存在实数![]() 满足:
满足:![]() ,
,![]() ,并且使得不等式
,并且使得不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)当
;(II)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;(III)
;(III)![]() .
.
【解析】
试题分析:(I)令![]() ,求得
,求得![]() ,求导代入
,求导代入![]() 可得斜率为
可得斜率为![]() .
.![]() 与
与![]() 轴交于点
轴交于点![]() ,求导代入
,求导代入![]() 可得斜率为
可得斜率为![]() .两条直线平行,故
.两条直线平行,故![]() ,
,![]() ;(II)化简函数
;(II)化简函数![]() 可得
可得![]() .令
.令![]() ,利用导数并对
,利用导数并对![]() 进行分类讨论,可求得函数的最小值;(III)先求得
进行分类讨论,可求得函数的最小值;(III)先求得![]() ,利用导数可知
,利用导数可知![]() 在
在![]() 上单调递增,有
上单调递增,有![]() ,对
,对![]() 分成
分成![]() 类进行分类讨论,求得其取值范围是
类进行分类讨论,求得其取值范围是![]() .
.
试题解析:
![]() 图象与
图象与![]() 轴异于原点的交点
轴异于原点的交点![]() ,
,![]()
![]() 图象与
图象与![]() 轴的交点
轴的交点![]() ,
,![]()
由题意可得![]() ,即
,即![]() ,
,
∴![]() ,
,![]()
(2)
![]() =
=![]()
令![]() ,在
,在 ![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,![]()
![]() 图象的对称轴
图象的对称轴![]() ,抛物线开口向上
,抛物线开口向上
①当![]() 即
即![]() 时,
时,![]()
②当![]() 即
即![]() 时,
时,![]()
③当![]() 即
即![]() 时,
时,
![]()
综上:当![]() 时,
时,![]() ;当
;当![]()
![]() ;当
;当![]() 时,
时,![]() …………8分
…………8分
![]() ,
,![]()
![]()
所以![]() 在区间
在区间![]() 上单调递增
上单调递增
∴![]() 时,
时,![]()
①当![]() 时,有
时,有![]() ,
,
![]() ,
,
得![]() ,同理
,同理![]() ,
,
∴ 由![]() 的单调性知
的单调性知 ![]()
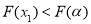 、
、![]()
从而有![]() ,符合题设.
,符合题设.
②当![]() 时,
时,![]() ,
,
![]() ,
,
由![]() 的单调性知
的单调性知 ![]()
![]() ,
,
∴![]() ,与题设不符
,与题设不符
③当![]() 时,同理可得
时,同理可得![]() ,
,
得![]() ,与题设不符.
,与题设不符.
∴综合①、②、③得![]()


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其它各面用钢筋网围成.
(1)现有可围![]() 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为![]() ,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?
,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
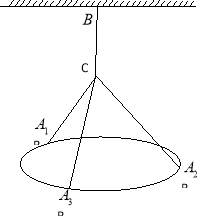
【题目】一吊灯下沿圆环直径为![]() 米,通过拉链
米,通过拉链![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() 、
、![]() 、
、![]() 是圆上三等份点)悬挂在
是圆上三等份点)悬挂在![]() 处,圆环呈水平状态并距天花板2米,如图所示.
处,圆环呈水平状态并距天花板2米,如图所示.
(1)为使拉链总长最短,![]() 应多长?
应多长?
(2)为美观与安全,在圆环上设置![]() ,
,![]() ,……,
,……,![]() (
(![]() )各等分点,仍按上面方法连接.若还要求拉链总长度最短,对比(1)时C点位置,此时C点将会上移还是会下移?请说明理由.
)各等分点,仍按上面方法连接.若还要求拉链总长度最短,对比(1)时C点位置,此时C点将会上移还是会下移?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量ξ服从正态分布N(0,σ2),P(ξ>2)=0.023,则P(-2≤ξ≤2)=( )
A. 0.954 B. 0.628 C. 0.477 D. 0.977
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S 相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
A.![]() 海里/时 B.
海里/时 B.![]() 海里/时
海里/时
C.![]() 海里/时 D.
海里/时 D.![]() 海里/时
海里/时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司招工需要遵循以下程序:
在招工前要明确招工事宜,如果是大学毕业的,需出示大学毕业证及身份证,填写应聘书,直接录取;如果不是大学毕业的,需要参加考试培训,首先要填写考生注册表,领取考生编号,明确考试科目和时间,然后缴纳考试费用,按规定时间参加考试,领取成绩单,如果成绩合格,被录用,并填写应聘书,成绩不合格不予录用,即落聘.
请设计一个流程图,表示这个公司的招工程序.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com