
某工厂生产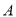 、
、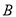 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于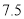 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各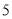 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
|
|
|
|
|
|
B |
|
|
|
|
|
由于表格被污损,数据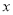 、
、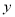 看不清,统计员只记得
看不清,统计员只记得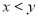 ,且
,且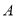 、
、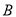 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中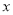 与
与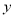 的值;
的值;
(2)从被检测的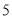 件
件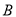 种元件中任取
种元件中任取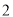 件,求
件,求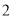 件都为正品的概率.
件都为正品的概率.
(1)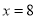 ,
,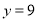 ;(2)
;(2)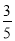 .
.
【解析】
试题分析:(1)根据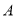 、
、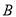 两种元件的检测数据的平均数与方差分别相等,利用平均数与方差的计算公式列方程组求出
两种元件的检测数据的平均数与方差分别相等,利用平均数与方差的计算公式列方程组求出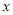 与
与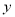 的值;(2)将
的值;(2)将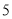 件
件 元件编号,并将说明哪些是正品,利用列举法将所有的基本事件与问题中涉及事件所包含的基本进行列举,然后利用古典概型的概率计算公式求出相应事件的概率.
元件编号,并将说明哪些是正品,利用列举法将所有的基本事件与问题中涉及事件所包含的基本进行列举,然后利用古典概型的概率计算公式求出相应事件的概率.
试题解析:(1)因为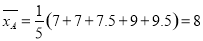 ,
,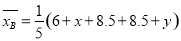 ,
,
由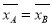 ,得
,得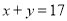 ,①
,①
因为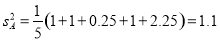 ,
,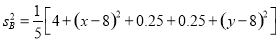 ,
,
由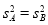 ,得
,得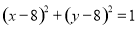 ,②
,②
由①②解得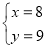 或
或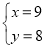 ,
,
因为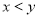 ,所以
,所以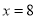 ,
,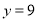 ;
;
(2)记被检测的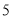 件的
件的 种元件分别为
种元件分别为 、
、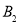 、
、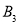 、
、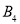 、
、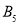 ,其中
,其中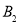 、
、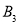 、
、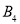 、
、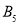 为正品,
为正品,
从中任取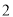 件,共有
件,共有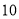 个基本事件,列举如下:
个基本事件,列举如下:
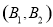 、
、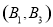 、
、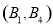 、
、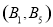 、
、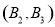 、
、 、
、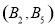 、
、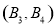 、
、 、
、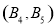 ,
,
记“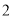 件都为正品”为事件
件都为正品”为事件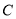 ,则事件
,则事件 包含以下
包含以下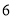 个基本事件:
个基本事件:
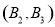 、
、 、
、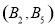 、
、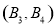 、
、 、
、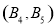 ,
,
 ,所以
,所以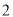 件都为正品的概率为
件都为正品的概率为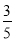 .
.
考点:1.平均数与方差;2.古典概型


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟理科数学试卷(解析版) 题型:选择题
定义域为R的四个函数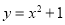 ,
,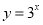 ,
, ,
, 中,偶函数的个数是( )
中,偶函数的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省汕头市高三3月高考模拟考试文科试卷(解析版) 题型:解答题
已知函数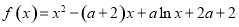 (其中
(其中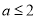 ).
).
(1)求函数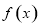 的单调区间;
的单调区间;
(2)若函数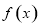 在
在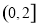 上有且只有一个零点,求实数
上有且只有一个零点,求实数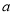 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检理科数学试卷(解析版) 题型:选择题
在实数集R中定义一种运算“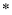 ”,对任意
”,对任意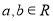 ,
,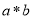 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质:
(1)对任意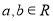 ,
,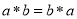 (2)对任意的
(2)对任意的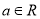 ,
,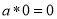 ;
;
(4)对任意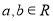 ,
,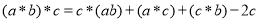
关于函数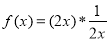 的性质,有如下说法:
的性质,有如下说法:
函数f(x)的最小值为3 函数f(x)为奇函数 函数f(x)的单调递增区间为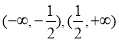 ,其中所有正确说法的个数( )
,其中所有正确说法的个数( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com