
已知函数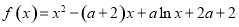 (其中
(其中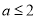 ).
).
(1)求函数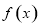 的单调区间;
的单调区间;
(2)若函数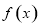 在
在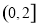 上有且只有一个零点,求实数
上有且只有一个零点,求实数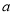 的取值范围.
的取值范围.
(1)详见解析;(2)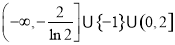 .
.
【解析】
试题分析:(1)先求函数 的定义域与导数
的定义域与导数 ,对
,对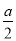 是否在定义域内以及在定义域内与
是否在定义域内以及在定义域内与 进行大小比较,从而确定函数的单调区间;(2)在(1)的条件下结合函数的单调性与零点存在定理对端点值或极值的正负进行限制,从而求出参数
进行大小比较,从而确定函数的单调区间;(2)在(1)的条件下结合函数的单调性与零点存在定理对端点值或极值的正负进行限制,从而求出参数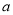 的取值范围.
的取值范围.
试题解析:(1)函数定义域为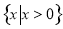 ,
,
 ,
,
①当 ,即
,即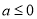 时,
时,
令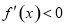 ,得
,得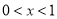 ,函数
,函数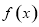 的单调递减区间为
的单调递减区间为 ,
,
令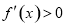 ,得
,得 ,函数
,函数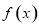 的单调递增区间为
的单调递增区间为 ;
;
②当 ,即
,即 时,
时,
令 ,得
,得 或
或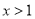 ,函数
,函数 的单调递增区间为
的单调递增区间为 ,
, ,
,
令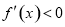 ,得
,得 ,函数
,函数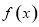 的单调递减区间为
的单调递减区间为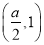 ;
;
③当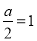 ,即
,即 时,
时, 恒成立,函数
恒成立,函数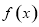 的单调递增区间为
的单调递增区间为 ;
;
(2)①当 时,由(1)可知,函数
时,由(1)可知,函数 的单调递减区间为
的单调递减区间为 ,
,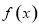 在
在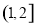 单调递增,
单调递增,
所以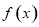 在
在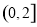 上的最小值为
上的最小值为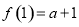 ,
,
由于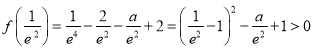 ,
,
要使 在
在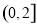 上有且只有一个零点,
上有且只有一个零点,
需满足 或
或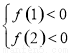 ,解得
,解得 或
或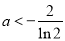 ,
,
所以当 或
或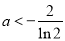 时,
时,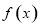 在
在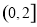 上有且只有一个零点;
上有且只有一个零点;
②当 时,由(1)可知,函数
时,由(1)可知,函数 在
在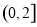 上单调递增,
上单调递增,
且 ,
,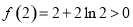 ,
,
所以当 时,
时, 在
在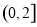 上有且只有一个零点;
上有且只有一个零点;
③当 时,由(1)可知,函数
时,由(1)可知,函数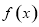 在
在 内单调递增,在
内单调递增,在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
又因为 ,所以当
,所以当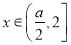 时,总有
时,总有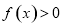 ,
,
因为 ,
,
所以 ,
,
所以 在区间
在区间 内必有零点,
内必有零点,
又因为 在
在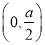 内单调递增,
内单调递增,
从而当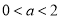 时,
时,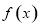 在
在 上有且只有一个零点,
上有且只有一个零点,
综上所述,当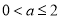 或
或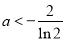 或
或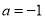 时,
时, 在
在 上有且只有一个零点.
上有且只有一个零点.
考点:1.函数的单调区间与导数;2.分类讨论;3.函数的零点;4.零点存在定理


科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟理科数学试卷(解析版) 题型:选择题
下列命题中,真命题是 ( )
A. ,
,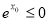 ;
;
B.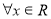 ,
,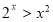 ;
;
C.“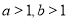 ”是“
”是“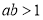 ”的充分不必要条件;
”的充分不必要条件;
D.设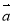 ,
,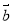 为向量,则“
为向量,则“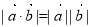 ”是“
”是“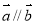 ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二理科数学试卷(解析版) 题型:选择题
对于任意两个正整数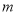 、
、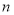 ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当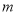 、
、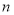 都是正奇数时,
都是正奇数时,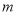 ※
※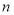 =
=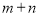 ;当
;当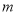 、
、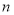 不全为正奇数时,
不全为正奇数时,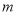 ※
※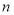 =
=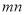 .则在此定义下,集合
.则在此定义下,集合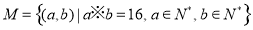 中的元素个数是( )
中的元素个数是( )
A.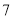 B.
B.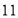 C.
C.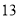 D.
D.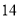
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二文科数学试卷(解析版) 题型:填空题
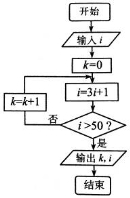
阅读如图所示的程序框图,若输入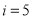 ,则输出的
,则输出的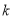 值为______________.
值为______________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省汕头市高三3月高考模拟考试文科试卷(解析版) 题型:解答题
某工厂生产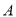 、
、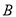 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于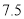 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各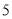 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
|
|
|
|
|
|
B |
|
|
|
|
|
由于表格被污损,数据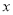 、
、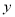 看不清,统计员只记得
看不清,统计员只记得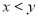 ,且
,且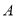 、
、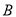 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中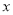 与
与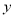 的值;
的值;
(2)从被检测的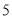 件
件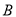 种元件中任取
种元件中任取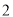 件,求
件,求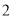 件都为正品的概率.
件都为正品的概率.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省汕头市高三3月高考模拟考试文科试卷(解析版) 题型:选择题
“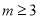 ”是“关于
”是“关于 、
、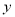 的不等式组
的不等式组 表示的平面区域为三角形”的( )
表示的平面区域为三角形”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检理科数学试卷(解析版) 题型:填空题
已知函数f(x)=x-[x],其中[x]表示不超过实数x的最大整数,若关于x的方程f(x)=kx+k有三个不同的实根,则实数k的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com