
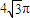 的球的表面上有A,B,C三点,
的球的表面上有A,B,C三点,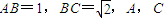 两点的球面距离为
两点的球面距离为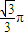 ,则球心到平面ABC的距离为 .
,则球心到平面ABC的距离为 .  阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(辽宁卷理14文14)在体积为![]() 的球的表面上有A,B,C三点,AB=1,BC=
的球的表面上有A,B,C三点,AB=1,BC=![]() ,A,C两点的球面距离为
,A,C两点的球面距离为![]() ,则球心到平面ABC的距离为_________.
,则球心到平面ABC的距离为_________.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一暑假作业(三)必修2数学试卷(解析版) 题型:选择题
三棱锥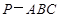 的四个顶点都在体积为
的四个顶点都在体积为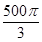 的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )
的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )
A.7 B.7.5 C.8 D.9
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第二次月考理科数学试卷 题型:选择题
在体积为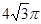 的球的表面上有A,B,C三点,AB=1,BC=
的球的表面上有A,B,C三点,AB=1,BC=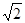 ,A,C两点的球面距离为
,A,C两点的球面距离为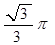 ,则球心到平面ABC的距离为
( )
,则球心到平面ABC的距离为
( )
A.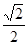 B.
B.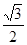 C.
C.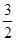 D.1
D.1
查看答案和解析>>
科目:高中数学 来源:2010-2011学年云南省昆明市高三第三次月考理科数学试卷 题型:填空题
在体积为 的球的表面上有A、B、C三点,
的球的表面上有A、B、C三点, ,A、C两点的球面距离为
,A、C两点的球面距离为 ,则球心到平面ABC的距离为
。
,则球心到平面ABC的距离为
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com