练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题14分）设为实数，函数.(1)若，求的取值范围；(2)求的最小值；(3)设函数，直接写出(不需给出演算步骤)不等式的解集.

    答案

    （3）时，得，

    当时，；…………………………10分

    当时，△>0,得：……………11分

    讨论得：当时，解集为;

    当时，解集为;

    当时，解集为.…………………………14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本题满分14分）已知定义在的函数（为实常数）．

    （Ⅰ）当时，证明：不是奇函数；（Ⅱ）设是奇函数，求与的值；

    （Ⅲ）当是奇函数时，证明对任何实数、c都有成立．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省高三第二次阶段性考试数学试卷（解析版） 题型：解答题

    (本题满分14分) 已知是方程的两个不等实根，函数的定义域为．

    ⑴当时，求函数的值域；

    ⑵证明：函数在其定义域上是增函数；

    ⑶在（1）的条件下，设函数，

    若对任意的，总存在，使得成立，

    求实数的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省高三第一次月考理科数学试卷（解析版） 题型：解答题

    (本题满分14分)设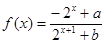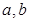（为实常数）．

    （1）当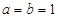时，证明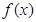：不是奇函数；

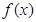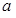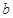    （2）设是奇函数，求与的值；

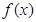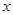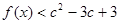    （3）当是奇函数时，证明对任何实数、c都有成立

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年上海市闵行区高三上学期期末质量抽测理科数学试卷 题型：解答题

    （本题满分14分）本题共有2个小题，第(1)小题满分5分，第(2)小题满分9分．

    设双曲线，是它实轴的两个端点，是其虚轴的一个端点.已知其一条渐近线的一个方向向量是，的面积是，为坐标原点，直线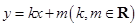与双曲线C相交于、两点，且．

    （1）求双曲线的方程；

    （2）求点的轨迹方程,并指明是何种曲线.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题14分）函数(为实数，)，，

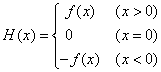
      ⑴ 若，且方程有唯一实根，求的表达式；

      ⑵ 在⑴的条件下，当时，是单调函数，求实数取值范围；

      ⑶ 设且，解关于m的不等式： 。

    查看答案和解析>>

    同步练习册答案