
分析 (Ⅰ)因为a有3种取法,b有5种取法,则对应的函数有3×5=15个,函数f(x)的图象关于直线x=$\frac{2b}{a}$对称,若事件A发生,则a>0且$\frac{2b}{a}$≤1,由此利用列举法能求出A发生的概率.
(Ⅱ)集合{(a,b)|a+4b-6≤0,a>0,b>0}对应的平面区域为Rt△AOB,由此利用几何概型能求出B 发生的概率.
解答 解:(Ⅰ)因为a有3种取法,b有5种取法,则对应的函数有3×5=15个.(2分)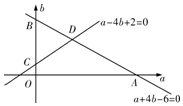
因为函数f(x)的图象关于直线x=$\frac{2b}{a}$对称,若事件A发生,则a>0且$\frac{2b}{a}$≤1.(3分)
数对(a,b)的取值为(1,-1),(2,-1),(2,1),(3,-1),(3,1)共5种.(5分)
所以P(A)=$\frac{5}{15}$=$\frac{1}{3}$.(6分)
(Ⅱ)集合{(a,b)|a+4b-6≤0,a>0,b>0}对应的平面区域为Rt△AOB,
如图.其中点A(6,0),B(0,$\frac{3}{2}$),
则△AOB的面积为$\frac{1}{2}$×$\frac{3}{2}$×6=$\frac{9}{2}$.(8分)
若事件B发生,则f(1)<0,即a-4b+2<0.(9分)
所以事件B对应的平面区域为△BCD.
由$\left\{\begin{array}{l}a+4b-6=0\\ a-4b+2=0\end{array}$,得交点坐标为D(2,1).
又C(0,$\frac{1}{2}$),则△BCD的面积为$\frac{1}{2}$×($\frac{3}{2}$-$\frac{1}{2}$)×2=1.
所以P(B)=$\frac{S△BCD}{S△AOB}$=$\frac{2}{9}$.(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法和几何概型的合理运用.


科目:高中数学 来源: 题型:解答题
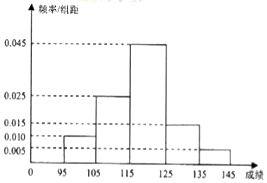 高二数学ICTS竞赛初赛考试后,某校对95分以上的成绩进行统计,其频率分布直方图如图所示,其中[135,145]分数段的人数为2人.
高二数学ICTS竞赛初赛考试后,某校对95分以上的成绩进行统计,其频率分布直方图如图所示,其中[135,145]分数段的人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
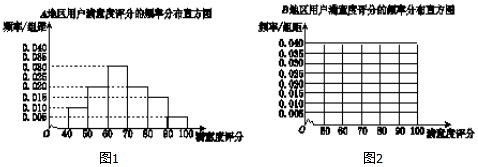
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 14 | 10 | 6 |
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=2n-1 | B. | an=3n | C. | 2 | D. | an=5n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com