
若某双曲线的焦点在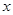 轴上,且实轴长、虚轴长、焦距成等差数列,则该双曲线的渐近线方程为( )
轴上,且实轴长、虚轴长、焦距成等差数列,则该双曲线的渐近线方程为( )
A.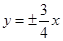 B.
B.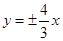 C.
C.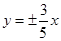 D.
D.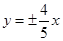
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:022
给出问题:F1、F2是双曲线![]() 的焦点,点P的双曲线上,若点P到焦点F1的距离等于9,求点P到焦点F2的距离,某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17,该学生的解答是否正确?若正确,请将它的解题依据填在下面空格内,若不正确,将正确的结果填在下面空格内______________.
的焦点,点P的双曲线上,若点P到焦点F1的距离等于9,求点P到焦点F2的距离,某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17,该学生的解答是否正确?若正确,请将它的解题依据填在下面空格内,若不正确,将正确的结果填在下面空格内______________.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:022
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com