练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    类比余弦定理，在△DEF中有余弦定理：DE2=DF2+EF2-2DF•EF∠DFE．拓展到空间，类比三角形的余弦定理，写出斜三棱柱ABC-A1B1C1BC的3个侧面面积之间的关系式（其中θ为侧面为ABB1A1与BCC1B1所成的二面角的平面角）
    S△A1C1C2=S△BB1A12+S四边形BCC1B12-2S△BB1A1•S四边形BCC1B1•cosθ
    S△A1C1C2=S△BB1A12+S四边形BCC1B12-2S△BB1A1•S四边形BCC1B1•cosθ
    ．
    分析：类比三角形的余弦定理，利用类比的方法写出斜三棱柱ABC-A1B1C1BC的3个侧面面积之间的关系式即可．
    解答：解：根据题意得：S△A1C1C2=S△BB1A12+S四边形BCC1B12-2S△BB1A1•S四边形BCC1B1•cosθ．
    故答案为：S△A1C1C2=S△BB1A12+S四边形BCC1B12-2S△BB1A1•S四边形BCC1B1•cosθ
    点评：此题考查了余弦定理，利用了类比推理，弄清余弦定理的结构特征是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：设计选修数学－1-2苏教版 苏教版 题型：047

    如图，点D为斜三棱柱ABC－A1B1C1的侧棱BB1上一点，DM⊥BB1交AA1与点M，DN⊥BB1交CC1于点N．

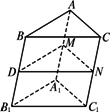
    (1)求证：CC1⊥MN；

    (2)在任意△DEF中有余弦定理：

    DE2＝DF2＋EF2－2DF·EFcos∠DFE，拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源：2014届浙江省高二（2-6班）下期中考试数学卷（解析版） 题型：填空题

    在平面内，余弦定理给出了三角形的三条边与其中一个角的关系，如： ，把四面体V-BCD与三角形作类比，设二面角V-BC-D，V-CD-B， V-BD-C，C-VB-D，B-VC-D，B-VD-C的大小依次为我们可以得到“四面体的余弦定理”：_____________________.（只需写出一个关系式）

     

    查看答案和解析>>

    同步练习册答案