下列判断错误的是( )
A.“am2<bm2”是“a<b”的充分不必要条件
B.命题“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1>0”
C.若p,q均为假命题,则p∧q为假命题
D.若ξ~B(4,0.25)则Dξ=1
【答案】
分析:本题考查了充分必要条件的判断、全称命题的否定、复合命题的判断和方差等多个知识点,命题A判不必要时,可取特值m
2=0,B、C考查的基本概念,命题D可由公式Dξ=np(1-p)求解.
解答:解:由am
2<bm
2知m
2≠0,不等式两边同乘以
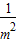
得,a<b,反之,若a<b,则取m
2=0时不能得到am
2<bm
2,
故am
2<bm
2是a<b的充分不必要条件,故A正确.
因为“?x∈R,x
3-x
2-1≤0”是全称命题,故其否定是特称命题,为“?x∈R,x
3-x
2-1>0”,故B正确.
若p,q均为假命题,则p∧q为假命题,故C正确.
如果随机变量ξ~B(4,0.25),则Eξ=4×0.25=1,Dξ=4×0.25(1-0.25)=0.75,所以D不正确.
故选D
点评:本题以考查课本基本知识为主,只要牢记基础知识,基本方法和基本公式就能做出正确解答,属于基础题.

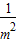 得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,
得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,
