Question

素材1：直线l₁:12x+6y-72=0.

素材2：直线l₂:ax+y-2=0.

先将上面的素材构建成一个问题，然后再解答.

Answer 1

构建问题：直线l₁:12x+6y-72=0,直线l₂:ax+y-2=0.

若上述两直线l₁、l₂与x、y轴的正半轴围成的四边形有外接圆，求外接圆的方程.

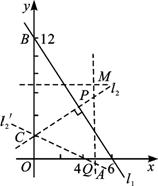
解析：设直线l₁与x、y轴的交点分别为A（6，0）、B（0，12），直线l₂与y轴的交点为C（0，2）.

（1）当l₁⊥l₂时，设垂足为P，又OA⊥OC.

∴四点O、A、P、C共圆且以AC为直径.

∴所求方程为x(x-6)+y(y-2)=0，即x²+y²-6x-2y=0.

（2)当l₁与l₂不垂直时，设l₂与x轴的正半轴交于点Q，若A、B、C、Q四点共圆，

则|OQ|·|OA|=|OC|·|OB|，

∴|OQ|=4.∴圆心M在线段BC、QA的中垂线上.∴M(5，7).

又|MA|=，

∴所求圆的方程为（x-5）²+(y-7)²=50.