练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设AB＝6，在线段AB上任取两点(端点A、B除外)，将线段AB分成了三条线段，

    (1)若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形的概率；

    (2)若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形的概率．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：吉林省长春市十一高中2009-2010学年高二上学期期中考试数学理科试题 题型：044

    已知抛物线C的顶点在原点，焦点F在x轴正半轴上，设A、B是抛物线C上的两个动点(AB不垂直于x轴)，且|AF|＋|BF|＝8，线段AB的中垂线恒过定点Q(6，0)，求此抛物线的方程．

    查看答案和解析>>

    科目：高中数学 来源：高考零距离　二轮冲刺优化讲练　数学 题型：044

    如图所示，在直角梯形P1DCB中，P1D∥CB，CD⊥P1D，且P1D＝6，BC＝3，DC＝，A是P1D的中点，沿AB把平面P1AB折起到平面PAB的位置，使二面角P－CD－B成角．设E、F分别是线段AB、PD的中点．

    (1)

    求证：AF∥平面PEC

    (2)

    求PC与底面所成角的正弦值

    查看答案和解析>>

    科目：高中数学 来源：浙江省宁波市鄞州区2012届高三高考适应性考试(3月)数学理科试题 题型：044

    如图，在直角梯形ABCP中，AB＝BC＝3，AP＝6，CD⊥AP于D，现将△PCD沿线段CD折成60°的二面角P－CD－A，设E，F，G分别是PD，PC，BC的中点．

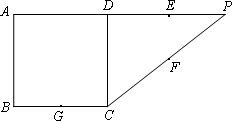
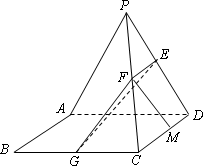
    (Ⅰ)求证：PA∥平面EFG；

    (Ⅱ)若M为线段CD上的动点，问点M在什么位置时，直线MF与平面EFG所成角为60°．

    查看答案和解析>>

    同步练习册答案