练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设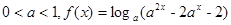，则使f(x)<0的x的取值范围为_____。

     

    【答案】

     

    【解析】

    试题分析：因为，那么可知f(x)<0时，则要满足

    ，那么设，故解得t>3,t<-1，即可知>3,<-1(舍)，那么根据指数函数单调性得到a的范围是，故填写。

    考点：本题主要考查了对数函数的不等式的求解运用。

    点评：解决该试题的关键是对于形如二次函数的指数不等式的求解运用。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设二次函数 y=f（x）=ax2+bx+c的图象以y轴为对称轴，已知a+b=1，而且若点（x，y）在 y=f（x）的图象上，则点（x，y2+1）在函数 g（x）=f[f（x）]的图象上．
    （1）求g（x）的解析式；
    （2）设F（x）=g（x）-λf（x），问是否存在这样的l（λ∈R），使f（x）在(-∞，-
    		2
    2
    )    内是减函数，在（-
    		2
    2
    ，0）内是增函数．

    查看答案和解析>>

    科目：高中数学 来源：河南省镇平一高2012届高三下学期第三次周考数学理科试题 题型：013

    设f(x)的定义域为D，若f(x)满足下面两个条件，则称f(x)为闭函数．①f(x)在D内是单调函数；②存在[a，b]D，使f(x)在[a，b]上的值域为[a，b]．如果f(x)＝＋k为闭函数，那么k的取值范围是

    [　　]

    A．k＜l

    B．≤k＜1

    C．k＞－1

    D．

    －1＜k≤－

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年北京师大附中高一（上）期中数学试卷（解析版） 题型：解答题

    设二次函数 y=f（x）=ax2+bx+c的图象以y轴为对称轴，已知a+b=1，而且若点（x，y）在 y=f（x）的图象上，则点（x，y2+1）在函数 g（x）=f[f（x）]的图象上．
    （1）求g（x）的解析式；
    （2）设F（x）=g（x）-λf（x），问是否存在这样的l（λ∈R），使f（x）在内是减函数，在（，0）内是增函数．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省镇平一高高三下学期第三次周考理科数学试卷 题型：选择题

    设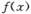的定义域为D，若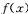满足下面两个条件，则称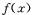为闭函数.①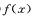在D内是单调函数;②存在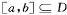，使f(x)在[a,b]上的值域为[a,b].如果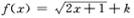为闭函数，那么k的取值范围是

    A.k<l    B.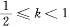    C. k >-1    D.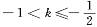

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设二次函数 y=f（x）=ax2+bx+c的图象以y轴为对称轴，已知a+b=1，而且若点（x，y）在 y=f（x）的图象上，则点（x，y2+1）在函数 g（x）=f[f（x）]的图象上．
    （1）求g（x）的解析式；
    （2）设F（x）=g（x）-λf（x），问是否存在这样的l（λ∈R），使f（x）在(-∞，-
    		2
    2
    )    内是减函数，在（-
    		2
    2
    ，0）内是增函数．

    查看答案和解析>>

    同步练习册答案