
【题目】在直角坐标系xOy中,已知点A(0,3)和B(6,0).
(Ⅰ)求线段AB垂直平分线的方程;
(Ⅱ)若曲线C上的任意一点P满足2|PA|=|PB|,求曲线C的方程.
 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】长郡中学早上8点开始上课,若学生小典与小方匀在早上7:40至8:00之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小典比小方至少早5分钟到校的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧棱PA⊥平面ABCD,E为AD的中点,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1; 
(1)求二面角C﹣PB﹣E的余弦值;
(2)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个判断: ①某校高三一班和高三二班的人数分别是m,n,某次测试数学平均分分别是a,b,则这两个班的数学平均分为 ![]() ;
;
②10名工人某天生产同一零件的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
③从总体中抽取的样本为 ![]() ,则回归直线
,则回归直线 ![]() 必过点(
必过点( ![]() )
)
④已知ξ服从正态分布N(0,σ2),且P(﹣2≤ξ≤0)=4,则P(ξ>2)=0.2
其中正确的个数有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三第一学期期末四校联考数学第I卷中共有8道选择题,每道选择题有4个选项,其中只有一个是正确的;评分标准规定:“每题只选一项,答对得5分,不答或答错得0分.”某考生每道题都给出一个答案,已确定有5道题的答案是正确的,而其余选择题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜,试求出该考生:
(1)得40分的概率;
(2)得多少分的可能性最大?
(3)所得分数ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数 ![]() ,其中a>0.设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.则b的最大值为( )
,其中a>0.设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.则b的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kex﹣x2(其中k∈R,e是自然对数的底数).
(Ⅰ)若k<0,试判断函数f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若k=2,当x∈(0,+∞)时,试比较f(x)与2的大小;
(Ⅲ)若函数f(x)有两个极值点x1 , x2(x1<x2),求k的取值范围,并证明0<f(x1)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: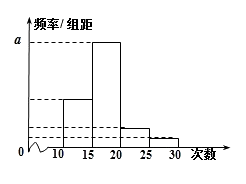

(1)求出表中M,P及图中 ![]() 的值;
的值;
(2)若该校高二学生有240人,试估计该校高二学生参加社区服务的次数在区间[10,15]内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30]内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com