
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点A(0,3)和B(6,0).
(Ⅰ)求线段AB垂直平分线的方程;
(Ⅱ)若曲线C上的任意一点P满足2|PA|=|PB|,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且f(x+2)=f(x﹣2);当0≤x≤1时,f(x)= ![]() ,则f(1)+f(2)+f(3)+…+f等于( )
,则f(1)+f(2)+f(3)+…+f等于( )
A.﹣1
B.0
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为 ![]() ,C、D两辆汽车每天出车的概率均为
,C、D两辆汽车每天出车的概率均为 ![]() ,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是
的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是 ![]() ,如图所示.
,如图所示.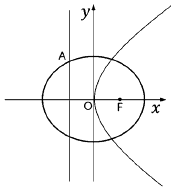
(1)求椭圆的标准方程;
(2)抛物线的准线与椭圆在第二象限相交于点A,过点A作抛物线的切线l,l与椭圆的另一个交点为B,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心(x0 , f(x0)),其中x0满足f″(x0)=0.已知函数f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,则f(
,则f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( ) 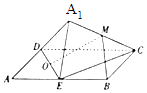
A.与平面A1DE垂直的直线必与直线BM垂直
B.异面直线BM与A1E所成角是定值
C.一定存在某个位置,使DE⊥MO
D.三棱锥A1﹣ADE外接球半径与棱AD的长之比为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com