【题目】抛物线y2＝4x的内接三角形的一个顶点在原点，三边上的高线都通过抛物线的焦点，求此三角形外接圆的方程．
科目：高中数学 来源： 题型：
【题目】下列四个判断： ①某校高三一班和高三二班的人数分别是m，n，某次测试数学平均分分别是a，b，则这两个班的数学平均分为 
；
②10名工人某天生产同一零件的件数分别是15，17，14，10，15，17，17，16，14，12，设其平均数为a，中位数为b，众数为c，则有c＞a＞b；
③从总体中抽取的样本为 
，则回归直线 
必过点（ 
）
④已知ξ服从正态分布N（0，σ2），且P（﹣2≤ξ≤0）=4，则P（ξ＞2）=0.2
其中正确的个数有（ ）
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=log2（3+x）﹣log2（3﹣x），
（1）求函数f（x）的定义域，并判断函数f（x）的奇偶性；
（2）已知f（sinα）=1，求α的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=aexlnx+ 
，曲线y=f（x）在点（1，f（1））处得切线方程为y=e（x﹣1）+2．
（Ⅰ）求a、b；
（Ⅱ）证明：f（x）＞1．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以
表示值域为R的函数组成的集合，
表示具有如下性质的函数
组成的集合：对于函数，存在一个正数
，使得函数的值域包含于区间
.例如，当
，
时，
，
.现有如下命题：
①设函数
的定义域为
，则“
”的充要条件是“
，
，
”；
②函数
的充要条件是有最大值和最小值；
③若函数，
的定义域相同，且，
，则
；
④若函数
（
，
）有最大值，则.
其中的真命题有 .（写出所有真命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆 
的离心率为 
，且椭圆C上的点到椭圆右焦点F的最小距离为 
.
（1）求椭圆C的方程；
（2）过点F且不与坐标轴平行的直线l与椭圆C交于A,B两点，线段AB的中点为M， O为坐标原点，直线 
的斜率分别为 
若成等差数列，求直线l的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对某校高二年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：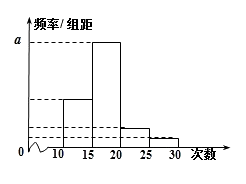
（1）求出表中M，P及图中 
的值；
（2）若该校高二学生有240人，试估计该校高二学生参加社区服务的次数在区间[10,15]内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[25,30]内的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法，进行了一次调研，得到了票价x(单位：元)与渴望观影人数y(单位：万人)的结果如下表：
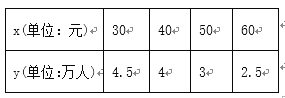
(1)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
(2)根据(1)中求出的线性回归方程，若票价定为70元，预测该电影院渴望观影人数．附：回归直线的斜率和截距的最小二乘法估计公式分别为：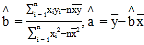
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
